Analytical Geometry

How To Check If A Point Is Inside A Rectangle?

The Area Method

1. Form a triangle between the point and every pair of consecutive vertices on the rectangle.
2. Calculate the area of this triangle
3. Sum up the areas of all of these triangles.
4. If the sum of these areas is greater than the area of the rectangle, then the point is outside the rectangle, else the sum of the areas must equal the area of the rectangle and the point is either inside or on the edge of the rectangle.
5. To differentiate between a point that is on the edge of the rectangle vs. one that is inside it, look at all the triangle areas. If any are 0, then the point is on the edge of the rectangle, otherwise it is inside the rectangle.

This method works not just for a rectangle but for any polygon!

The Angle Method

1. Travel around the vertices of the rectangle in a clockwise fashion.
2. For each line segment, calculate the angle between this line and a line formed from the point and the first vertex which makes up the line.
3. If all the angles are positive (incl. 0), then the point is inside the rectangle. If all the angles are positive and one or more is 0, then the point is on the edge of the rectangle (if one is 0, then it is on the edge, if two are 0, then the point is on one of the rectangle’s corners).
4. If one or more angles is negative, then the point is outside the rectangle.

The Product Of Vectors Method

This uses vector notation:

$(0 < AM \cdot AB < AB \cdot AB) \wedge (0 < AM \cdot AD < AD \cdot AD)$

where:
$A$, $B$ and $B$ are 3 adjacent vertices of the rectangle
$M$ is the vector representation of the point that could be inside the rectangle
$<$ is the logical less-than operator
$\wedge$ is the logical AND operator

Notice that this method does not use point C at all! It projects the point M onto the line AB and AD and makes sure that these projections lie somewhere on the line.

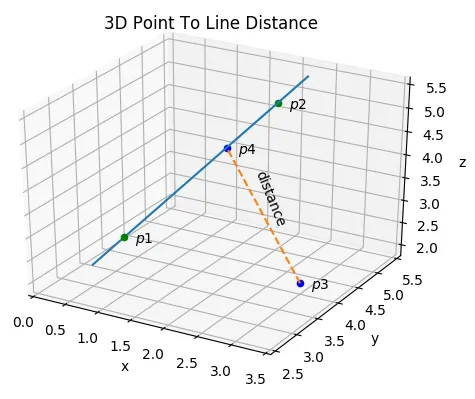
How To Find The Distance Between A Line And A Point In 3D

Given two points $x_1$ and $x_2$ which form a line in 3D space, and a third point $x_0$ in 3D space, the shortest distance $d$ between the point $x_0$ and the line is given by:

$d = \frac{|(x_0 - x_1) \times (x_0 - x_2)|}{|x_2 - x_1|}$

where:
$\times$ is the cross-product
$| vector |$ is the magnitude of the vector

The Long Way

Assume we have points $\mathbf{p1}$ and $\mathbf{p2}$ which form a line, and we want to find the shortest distance from this line to a point $\mathbf{p3}$.

A diagram showing a 3D point to line distance problem.

We will first find the point $\mathbf{p4}$ which is the closest point to $\mathbf{p3}$ which is on the line. Once we have this, finding the distance of the line which goes from $\mathbf{p3}$ to $\mathbf{p4}$ will be trivial.

The point $\mathbf{p4}$ can be expressed in parametric form using the equation for a line from $\mathbf{p1}$ to $\mathbf{p2}$:

\mathbf{p4} = u(\mathbf{p2} - \mathbf{p1}) \label{eq:point4} \tag{1}

We want to find $u$ so we can then find $P4$. Since there are two unknowns, we will need another equation. We can form one from the knowledge that the $P1 P2$ line and the line that connects the point $P3$ to this line will be perpendicular, which means that the dot product will be 0. We can write this as:

\begin{equation} (\mathbf{p3} - \mathbf{p4}) \bullet (\mathbf{p2} - \mathbf{p1}) = 0 \label{eq:dot-product} \tag{2} \end{equation}

Substituting $\eqref{eq:point4}$ into $\eqref{eq:dot-product}$ gives us:

(\mathbf{p3} - \mathbf{p1} - u(\mathbf{p2} - \mathbf{p1})) \bullet (\mathbf{p2} - \mathbf{p1}) = 0 \label{eq:substituted} \tag{3}

Expanding $\eqref{eq:substituted}$ gives us:

$\mathbf{p3} \bullet (\mathbf{p2} - \mathbf{p1}) - \mathbf{p1} \bullet (\mathbf{p2} - \mathbf{p1}) - u(\mathbf{p2} - \mathbf{p1})\bullet(\mathbf{p2} - \mathbf{p1}) = 0$

Factorizing and realizing that $(\mathbf{p2} - \mathbf{p1})\bullet(\mathbf{p2} - \mathbf{p1})$ is the norm squared:

$(\mathbf{p3} - \mathbf{p1}) \bullet (\mathbf{p2} - \mathbf{p1}) - u\Vert\mathbf{p2} - \mathbf{p1}\Vert^2 = 0$

Re-arrange for $u$:

$u = \frac{(\mathbf{p3} - \mathbf{p1}) \bullet (\mathbf{p2} - \mathbf{p1})}{\Vert\mathbf{p2} - \mathbf{p1}\Vert^2}$

We can now work out a value for $u$, given the values of the three points we know! Once a value for $u$ is found, we can then calculate the location of point $\mathbf{p4}$ using $\eqref{eq:point4}$.

Once $\mathbf{p4}$ is found, the distance between the point $\mathbf{p3}$ and the line is simply the distance of the line $\mathbf{p3p4}$:

$d = \Vert\mathbf{p4} - \mathbf{p3}\Vert$

How To Calculate The Angle Between Two Lines In 3D

The one is relatively easy. Given the lines $l_1 = a_1 t + b_1$ (both are in parametric form), we can use the dot product rule. We don’t need to use $`b_1`$ or $b_2$, we just need the directional component of each line, $a_1$ and $a_2$ (think of these as the vectors for each line). Then we can use the dot product rule, and we just need to solve for $\theta$:

$\cos \theta = \frac{\b{a} \cdot \b{b}}{|\b{a}||\b{b}|}$