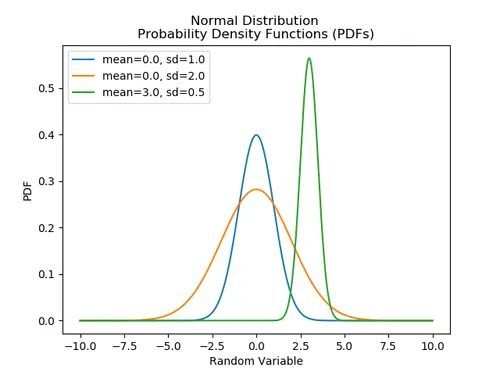
Normal Distributions

Geoffrey Hunter

mbedded.ninja Author

Probability Density Function

The probability density function of a normal distribution is given by:

$f(x, \mu | \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$

where:
$\mu$ is the mean of the distribution
$\sigma$ is the standard deviation

A few example probability density functions (PDFs) for the normal distribution.

See https://github.com/gbmhunter/BlogAssets/tree/master/Mathematics/Statistics/NormalDistribution for the code which generated these graphs.

Capped Normal Distribution

$\sigma_{overall}^2 = \frac{1}{\sqrt{2\pi} \sigma_{nd} + c} \left [\int_{-\infty}^{-c} +\int_{c}^{\infty} x^2 e^{(-\frac{1}{2} (\frac{x - c}{\sigma_{nd}})^2)} dx + \int_{-c}^{c} x^2 dx \right ]$

where:
$\sigma_{overall}$ is the standard deviation of the capped distribution
$\sigma_{nd}$ is the standard deviation of the normal distribution tails, ignoring the flat section in the middle
$c$ is the half-width of the flat section of the capped distribution
$x$ is the random variable