Latches and Flip-Flops

A latch or flip-flop (a.k.a. bistable multivibrator) is a digital circuit which is able to store a single “bit” of information. They are are key component in sequential logic (logic which depends not only on the present state on the inputs, but also past information). It has two stable states (representing a digital 1 or 0), and they can be made to change state by manipulating digital inputs. Hence they are also called bistable multivibrators (two stable states). Latches and flip-flops form the basic storage element in sequential logic. This page assumes a working knowledge of digital gates such as AND gates, OR gates, e.t.c. See the Gates page if you want to get up to speed on those first!

There is a lot of debate on what constitutes a latch vs. a flip-flop. We will adhere to the following definition:

• Latches are either completely asynchronous and they act immediately when their inputs change, or they are synchronous and provided a control signal which gates the latch so that it only acts when the control signal is a certain level (level-triggered) (the control signal called be called a clock). They are never edge-triggered.
• Flip-flops are fed a clock-signal, and only act the transition of the clock signal between states (edge-triggered). Just like some latches, flip-flops are synchronous.

We’re talking about the flip-flops on the right, not the left. If you’re not following along, don’t worry, this is a New Zealand thing :-D.

There is some confusing statements made in online references to the difference between latches and flip-flops. Some sources say latches are level-triggered and flip-flops are edge-triggered, but then go on to present a “D-type flip-flop” schematic which is actually level-triggered (normally transparent when the clock is high) and has no edge detection circuitry. Other sources say latches are not provided a clock whilst flip-flops need a clock, but then go to show a SR “latch” with an enable input, which could easily be driven by a clock signal.

Tip

Latches and flip-flops can store information, but they are not typically used when one generally thinks of computer “memory”, i.e. hard drives, solid-state drives or RAM. They use entirely different ways of storing information. Hard drives use magnetism to store non-volatile information, while solid-state drives and RAM use “floating gate” MOSFETs to store information.

Latches

Latches are asynchronous or level-triggered synchronous circuits which can retain memory. For latches that have an enable input, when a latch passes the input through to the output, we say it is transparent. When the input is blocked from passing through to the output (i.e. in input has no effect) we say the latch is opaque.

Most latches are built from two identical cross-coupled inverting logic gates, e.g. two NOR gates or two NAND gates.

SR Latches

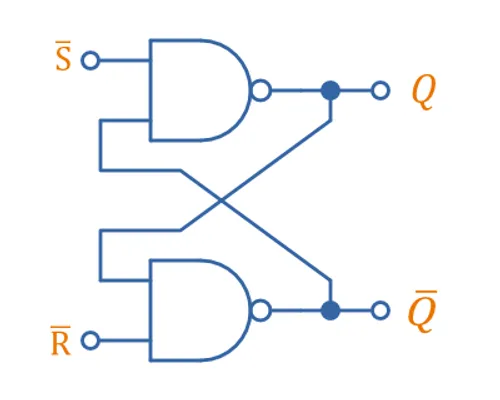
The SR (Set-Reset) latch is the most basic form of latch. It can be built from two cross-coupled NOR gates as shown below:

A SR latch made from NOR gates.

Driving either S or R high allows you to set the latch into the 1 or 0 state respectively. The state of the latch is represented by the output $Q$ and it’s complement $\bar{Q}$. Because of feedback from the outputs, driving both S and R low makes the latch “remember” or “retain” it’s last known state (holding). Below is the characteristic table for a SR latch built from NOR gates:

S	R	$Q_{n+1}$	$\overline{Q_{n+1}}$	Action
0	0	$Q$	$\bar{Q}$	No change
0	1	0	1	Reset
1	0	1	0	Set
1	1	0	0	Not allowed

Driving both set and reset high is a forbidden state, as it makes both $Q$ and $\bar{Q}$ equal 0.

A SR latch can also be made with two NAND gates instead of two NOR gates:

A SR latch made from two NAND gates.

When making the SR latch from NAND gates the invalid state is now $\overline{S} = \overline{R} = 0$ and the hold state is $\overline{S} = \overline{R} = 1$, they switch positions compared to the SR latch built from NOR gates. This is also the reason why $S$ and $R$ have been renamed to $\overline{S}$ and $\overline{R}$. Below is the full truth table:

$\overline{S}$	$\overline{R}$	$Q_{n+1}$	$\overline{Q_{n+1}}$	Action
0	0	1	1	Not allowed
0	1	0	1	Reset
1	0	1	0	Set
1	1	$Q$	$\bar{Q}$	No change

You can play with the interactive NAND-gate based SR latch below:

(full page version)

Example

Let’s simulate a NAND-based SR latch in Micro-Cap. Here is the schematic:

The digital stimulus U1 drives R and U2 drives S. With the following sequence:

1. Both were set to start as both 1’s, which should put the latch in an indeterminate state (start-up).
2. After 10ns, we test the set functionality by driving R low while keeping S high, which should set the latch.
3. After 20ns, R is driven back high which should make the latch hold the previous state (set).
4. After 30ns, we test the reset by driving S low while keeping R high, which should reset the latch.
5. After 40ns, S is driven back high, which should make the latch hold the previous state (reset).

And here is the transient analysis, which agrees with the expected behaviour:

Tip

Quite nicely, Micro-Cap shows the indeterminate state between 0 and 10ns with lines at both the 0 and 1 level.

The Micro-Cap circuit file used to perform this simulation can be downloaded here.

SN74LS279 is a quad SR latch component by Texas Instruments. Two of the four latches have two set inputs, allowing for either to be active to set the latch (equivalent to an OR gate placed before a normal single set input SR latch).

SR latches can be used to make a switch debounce circuit.

Why Have Q And Q Bar?

You might wonder what the purpose of $\bar{Q}$ is, given it’s always the opposite of $Q$ and you generally think of the value of $Q$ representing the state of the latch. It’s because sometimes you do need the inverse of $Q$ in further logic, and so providing it saves an inverter. And it’s needed in the internal logic of the latch anyway, so it’s not of great cost to provide a pin for it on the package.

How Does An SR Latch Work?

1. $R$ is HIGH and $S$ is LOW: Since $R$ is high, the output of the top NOR gate is LOW. This LOW feeds into the bottom NOR gate, along with $S$ which is also LOW, thus the output of the bottom NOR gate is HIGH. This HIGH feeds into the top NOR gate, which will keep the circuit in this defined state, even if $R$ is then brought LOW. This gives the SR latch it’s memory.
2. $R$ is LOW and $S$ is HIGH: Because of the symmetry, the same things happens, but in reverse. $Q$ is HIGH and $\bar{Q}$ is LOW. Again, if $S$ goes low, the SR latch “remembers” and keeps it’s outputs in the same state.

(A): A SR latch in the reset state. (B): A SR latch in the set state. Red represents logical “1”, black logical “0”.

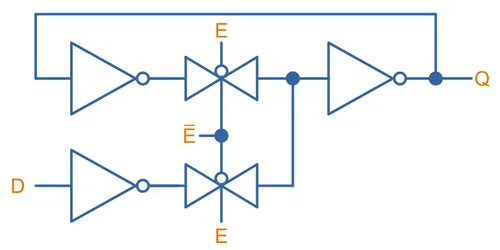
D Latch

A D Latch is like a SR latch except extra circuitry is added so that instead of and set and reset input, you obtain a single input to set or reset ($D$), and an enable line ($E$). This is generally a more practical type of latch as it can store the arbitrary state of a single line when told to do so by the enable input.

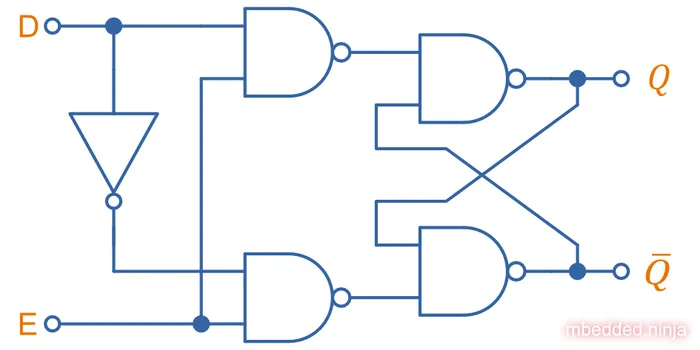
As the below diagram shows, a D latch is essentially a SR latch but with extra NAND gates and a inverter added to the front. The NAND gates “gate” the data line by anding it with the enable, such as that when the enable line is 0, no signal gets through. The inverter acts to remove the need to separate “set” and “reset” lines of a traditional SR latch by providing the two signals from one input.

A D latch made from NAND gates and an inverter.

You can see from the below truth table that when $E = 0$, the latch remembers it’s last state. When $E = 1$, the signal on $D$ is passed onto the output:

E	D	$Q_{n+1}$	$\overline{Q_{n+1}}$	Action
0	0	$Q$	$\bar{Q}$	No change
0	1	$Q$	$\bar{Q}$	No change
1	0	0	1	Reset
1	1	1	0	Set

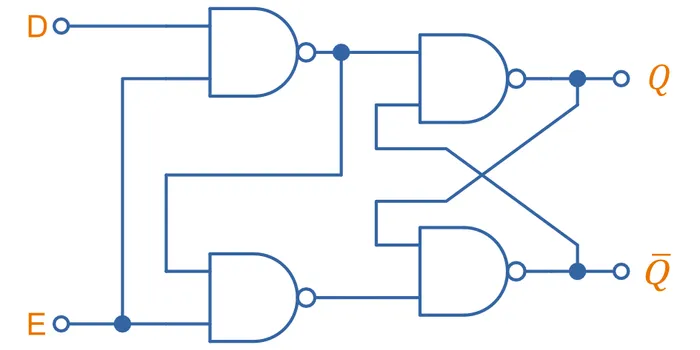
You can actually simplify the above circuit and remove the need for an inverter altogether. Just realise the output of the top left NAND gate is always the inverse of D as long as E is high, so you can actually take the output of this as the inverted D and feed it into the bottom left NAND gate as shown:

A simplified D latch without an inverter.

The above design, when built using CMOS technology would require 16 MOSFETs (4 for each NAND gate).

You can also make a D latch with inverters and transmission gates. This will result in a lower total transistor count to implement than the NAND gate style D latch above. The below schematic shows one way of doing it:

A D latch made from transmission gates.

The NAND gate implementation required 16 MOSFETs, but the above circuit only requires 12 (2 for each inverter, 2 for each transmission gate, and 2 to invert the enable signal to drive the transmission gates).

When $E$ is HIGH, the lower transmission gate is ON and the input $D$ is passed through to the output $Q$ via two inverters. When $E$ is LOW, the higher transmission gate is ON and the output is fed back to itself via two inverter (hence performing the latching action). The Texas Instruments CD4042B uses a similar technique to implement it’s D latches¹.

JK Latch

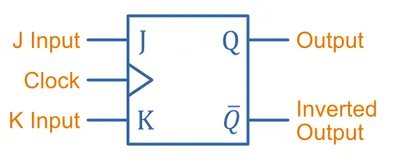
A JK latch is also known as the gated or clocked SR latch². It is a level-triggered device, even though many online tutorials suggest it is edge-triggered. Along with this, many references call this a JK flip-flop. Based on the rules we decided on above (latches for asynchronous or level-triggered devices, flip-flops for edge-triggered devices), we are calling this a latch. The schematic symbol is:

The schematic symbol for a JK latch.

Caution

The CLK input to a JK latch is traditionally drawn with a wedge symbol. The wedge symbol is normally associated with edge-triggered inputs, but the CLK input for a JK latch is level-triggered.

The letters J and K were chosen by the inventor of the JK latch, Jack Kilby³. A JK latch can be built with NAND gates with the following circuit:

Circuit showing how to build a JK latch from NAND gates.

Example

Let’s simulate a NAND-based JK latch in Micro-Cap. The schematic is:

The simulation schematic for the JK latch.

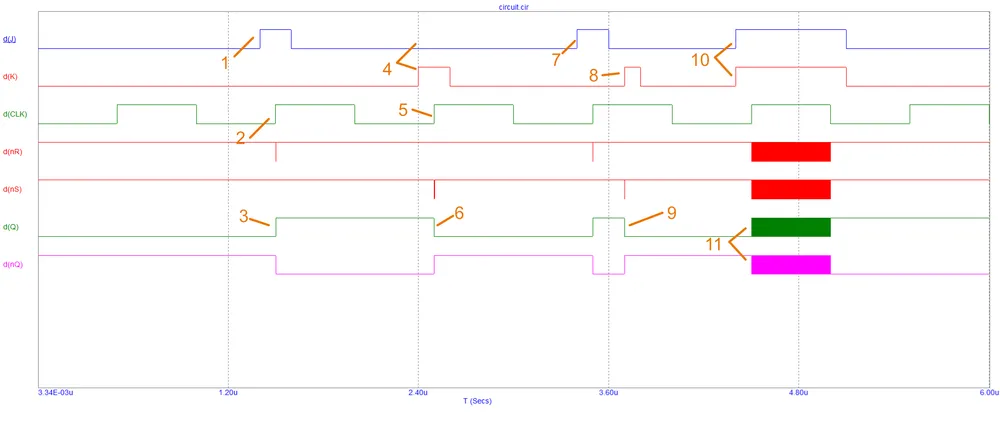
We have to set up some rather complicated digital stimulus to put the JK flip-flop through it’s paces. The simulation text determining these waveforms is:

The supported simulation “text” that goes with the schematic. This defines the waveforms of the 3x digital stimulus and the initial conditions.

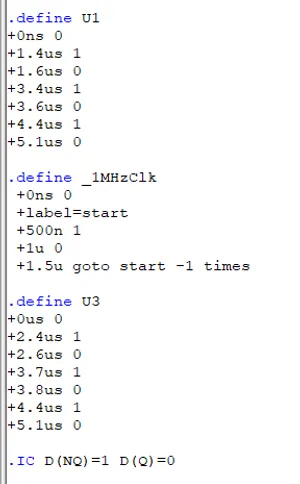
Notice also the definition of initial conditions at the bottom (.IC). If this was not provided, the states of Q and nQ would be forever stuck as indeterminate (in Micro-Cap this is represented by an X in text or double-lines at 0 and 1 in the waveform views), as the only way for the simulator to determine their state without using themselves (because of feedback) would be if nR or nS were 0 (because then the indeterminate state of Q and nQ doesn’t matter in determining Q and nQ, they would just be 1). However with a JK flip-flop we can’t set nR or nS to 0 via the inputs J and K without also considering the feedback from Q and nQ in the triple input NAND gates. Hence the circuit gets stuck! In real life, the circuit would settle on either Q=1 or Q=0 at start-up due to real-world noise and manufacturing differences in the start-up times of the NAND gates.

Below is the simulated waveforms of the circuit:

Annotated transient analysis of the JK flip-flop.

Explanation of behaviour:

1. To test setting the JK latch J is driven high, K is driven low whilst CLK is low (i.e. not enabled).
2. CLK goes high.
3. Q goes high due to J being high whilst CLK being high. Flip-flop has been set.
4. To test resetting the JK flip-flop, J is driven low and J driven high whilst CLK is low (not enabled).
5. CLK goes high.
6. Q gets reset as expected.
7. Let’s set the JK latch again, but this time show how it is not edge-triggered, the state can still be changed whilst the CLK is high.
8. We now bring J low and drive K high.
9. The output gets reset half-way through the CLK being high.
10. Lets demonstrate the oscillatory nature than can be caused if both J and K are high when the CLK is high.
11. The outputs oscillate at a speed determined by the propagation delay of the NAND gates!

Flip-Flops

Flip-flops are like latches, except their inputs are designed to accompanied with a clock signal, and they only change their outputs at clock edges (according to our naming rules we decided upon). Flip-flops typically require more circuitry to achieve the edge-triggered behaviour, but offer more versatility.

In popular literature, some level-triggered devices are commonly called flip-flops, especially the “JK flip-flop”.

Edge Detection

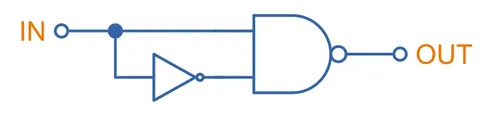
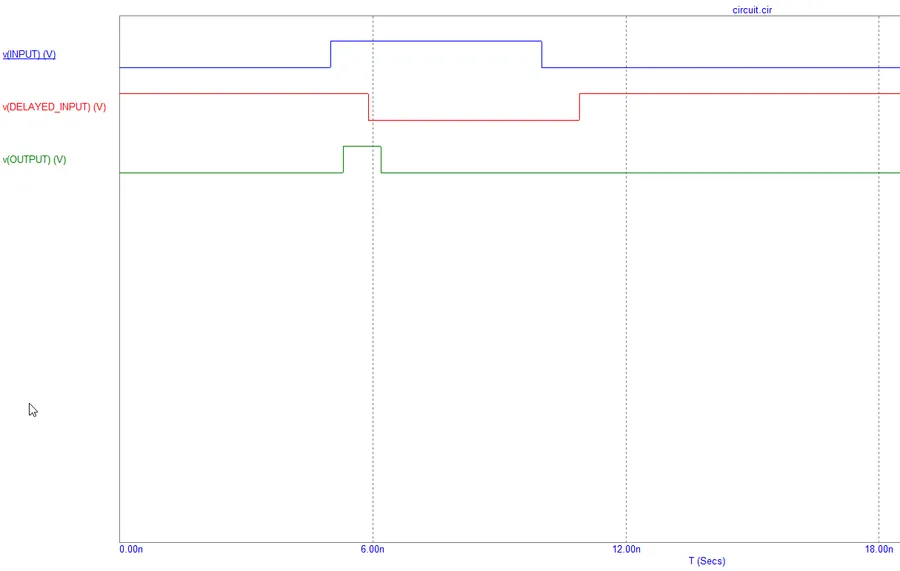
The key feature about flip-flops is that they are edge-triggered rather than level-triggered. So how do you design a flip-flop to only do something on the edges of the clock signal? One very simple way is a circuit made from an inverter and an AND gate, and exploits the non-zero propagation delay time through the inverter. When the input changes from a 0 to a 1, the delay through the inverter causes both of the inputs to go high for a brief amount of time, which makes the output 1. This enables the latch for a very brief amount of time during the positive edge transition.

This is the basic schematic:

Simple edge detection circuit made with an inverter and AND gate.

And this is what the timing looks like:

Positive edge-detecting circuit made from an inverter and an AND gate. This circuit exploits the non-zero propagation delay through the inverter.

Note

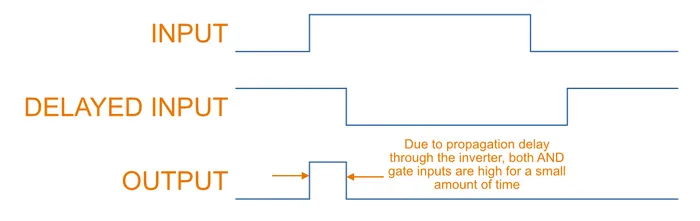
Any odd number of inverters may be placed in series to increase the pulse-width of the output signal. You commonly see this circuit drawn with three. An RC circuit may also be used to increase the pulse-width.

Example

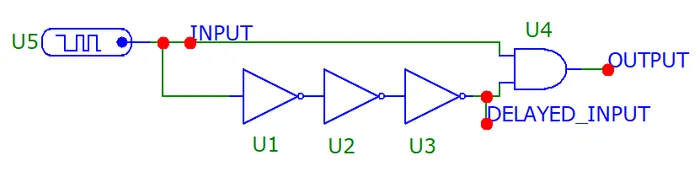
To test this idea, we can simulate the circuit in Micro-Cap. The schematic looks like this:

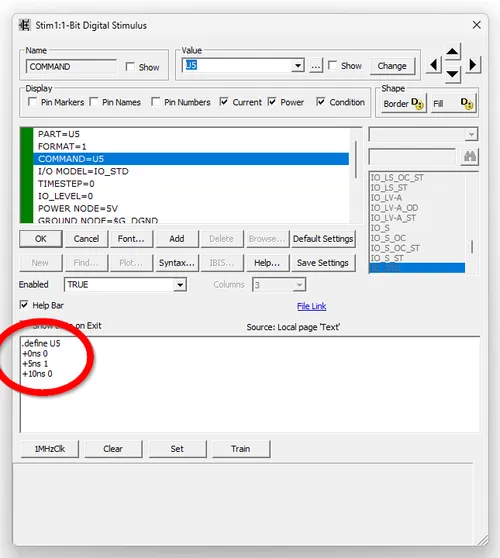
This simulation used logic gates which had a nominal delay time of 0.3ns (both low to high and high to low). This is the D_ABC timing model in Micro-Cap. The 1-bit Digital Stimulus was setup to go high at t=5ns and go low again at t=10ns as follows:

The resulting transient analysis is:

The Micro-Cap circuit file used to perform this simulation can be downloaded here.

The problem with the above edge-detection circuit is that it cannot guarantee that the created pulse is long enough for the latch logic to obtain the correct state⁴. There are better ways to create edge-triggered flip-flops, which we will show when we introduce the master-slave D-type flip-flop below.

D-Type Flip-Flops

A D-type flip-flop (where the D either stands for Delay or Data depending on who you ask) is a flip-flop which is based off the D latch, with additional circuitry to make it edge-triggered instead of level triggered. Below are the basic symbols for a D-type flip-flop:

The schematic symbols for a D-type flipflop. On the left is one WITH NO asynchronous set or reset, and the right is one WITH asynchronous set or reset.

Tip

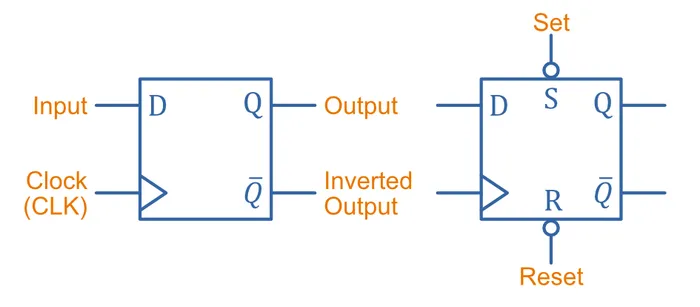
The wedge symbol drawn against the CLK input to tell the reader it is an edge-triggered input. Typically the set and reset are inverse logic, i.e. 1 to do nothing and 0 to either set or reset. The reset pin can also be called preset⁵.

D-type flip-flops are used for counters, shift-registers and input synchronization.

D-Type Flip-Flops with Inverters

But how is a D flip-flop actually made? Basically, you could add the edge-trigger circuit to the $E$ (enable) line of a D latch (as shown above) to make a D flip-flop:

A D flip-flop made from a D NAND-based latch and additional edge-trigger circuit made with an AND gate and inverter.

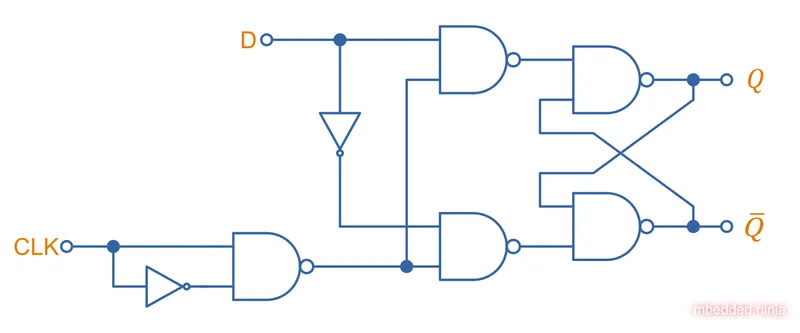
We now instead call the $E$ line the $CLK$, to signify it is edge-triggered rather than level-triggered.

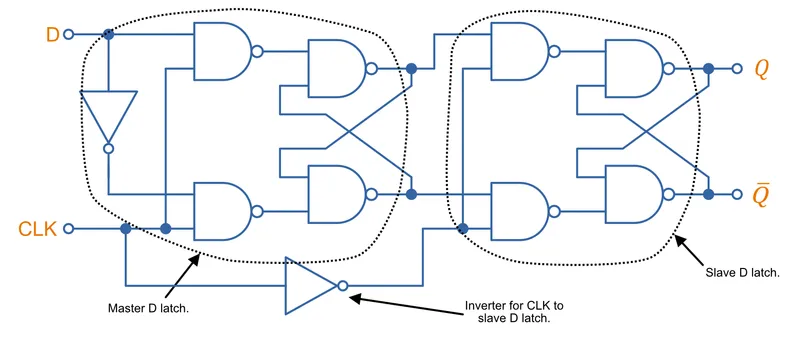
Master-Slave D Flip-Flop

Master-slave flip-flops are a another way of creating edge-triggered flip-flops from either level-triggered latches or flip-flops. Master-slave flip-flops are normally made from either two D flip-flops in series or two JK latches in series. The master is feed the raw clock signal (so is active while the clock is HIGH) whilst the slave is fed an inverted clock signal (and is active when the clock is LOW). Thus the master latch responds to the input while the clock is HIGH, and the slave is opaque. At the falling-edge of the clock, the master becomes opaque and slave becomes transparent, the master’s output is passed through the slave and onto the final output. This forms a negative edge-triggered flip-flop. The clock signal can be easily inverted to make a positive edge-triggered device.

A master-slave D flip-flop is made from connecting two D latches (edge-triggered) in series.

How a master-slave D flip-flop can be built from two D latches and a bit of additional logic.

Tip

Because we have the output and it’s inverse from the master latch, we don’t need the inverter at the input of the second latch, and can just wire to two connections straight through to the slave latch.

Below is an interactive simulation of negative edge-triggered master-slave D flip-flop. Click on the H (just below the D) to toggle the level of the data line, and watch the output change on the negative edge of the clock!

(full page version)

D-Type Flip-Flops with More NANDs

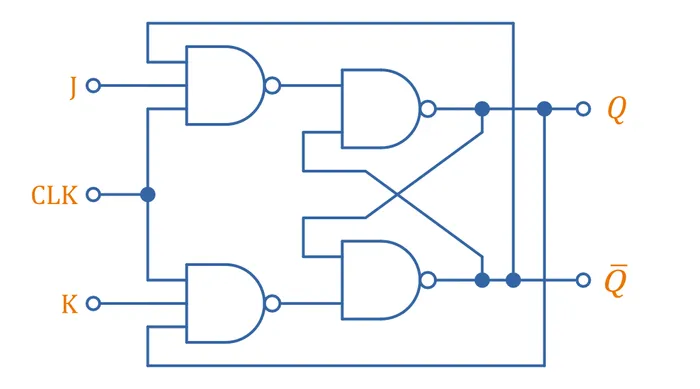
The above D-type master-slave flip-flop topology gives us reliable clock edge-triggered behaviour, but uses quite a few components (8 NAND gates + 2 inverters)! We can actually produce a functionality equivalent design with less components, with a clever arrangement of 6 NAND gates (of which 1 is 3-input, the rest 2-input). The logic diagram is:

A D-type flip-flop made solely from NAND gates. This version has no asynchronous set and clear inputs.

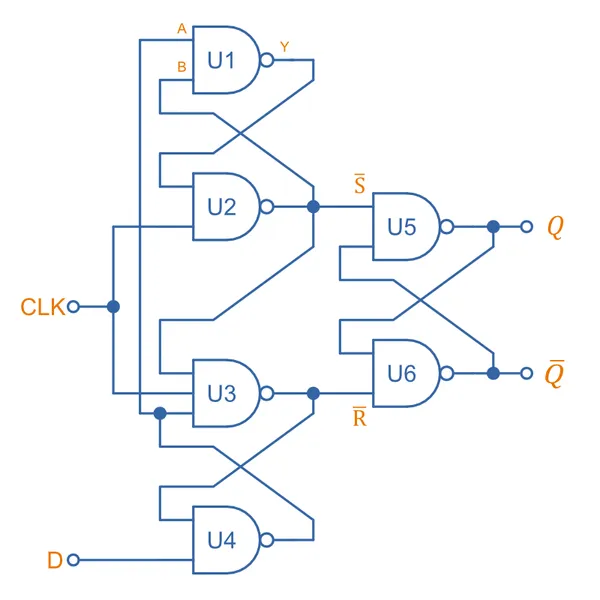
Roughly speaking, the above circuit is made from three SR latches, the output latch (center right), the input reset latch (upper left) and input set latch (lower left). Note that one of the input NAND gates is has three inputs rather than two.

Let’s try and understand how this circuit works! To do so, we’ll assume you know how the output SR latch works (if you don’t, read the first part of this page!). This removes U5 and U6 from the analysis, we can just treat their inputs as the standard R and S (as annotated on the diagram). Now let’s walk through two scenarios, the first when the CLK transitions from 0 to 1 while D=0, and then second scenario the same clock transition when D=1. We’ll see what happens to the circuit if further changes to D are made once the transition finishes (HINT: nothing happens!).

Tip

Common terminology for gates inputs/outputs are used where inputs are labelled UxA, UxB, … in order, and the output is UxY.

What if D=0 when CLK transitions from 0 to 1?

1. Before the transition, D=1 and CLK=0. Then at least 1 input to U2 and U3 is 0. This means than U2Y and U3Y must both be 1.
2. Since D=0 and U3Y=1, then U4Y=1.
3. Since U4Y=1 and U2Y=1, then U1Y=0. This gives the following state for all inputs/outputs:

   Gate	A	B	C	Y
   U1	1	1		0
   U2	0	0		1
   U3	1	0	1	1
   U4	1	0		1

4. Now, CLK transitions to 1. U2B and U3B immediately go high.
5. Within 1 propagation period, U2 and U3 respond. U2 doesn’t do anything because U2 still has at least 1 of it’s inputs as 0 (U2A). U3 however now has all three of it’s inputs high, and so U3Y=0. This gives the following state for all inputs/outputs:

   Gate	A	B	C	Y
   U1	1	1		0
   U2	0	1		1
   U3	1	1	1	0
   U4	0	0		1

6. If D now changes from 0 to 1 while the CLK is high, it will have no effect as it’s blocked at U4 by the fact U4A is now 0.

What if D=1 when CLK transitions from 0 to 1?

1. If D=1, CLK=0 then at least 1 input to U2 and U3 is 0. This means than U2Y and U3Y must both be 1.
2. Since D=1 and U3Y = 1, then U4Y=0.
3. Since U4Y=0 and U2Y=1, then U1Y=1.
4. The reset of the gate inputs/outputs are easy to deduce.
5. This gives the following state for all inputs/outputs:

   Gate	A	B	C	Y
   U1	0	1		1
   U2	1	0		1
   U3	1	0	0	1
   U4	1	1		0

6. Thus, R=1 and S=1, and so the output latch is in a hold state.
7. Now CLK immediately transitions to 1. Within 1 propagation delay, U2 and U3 respond. U2 already had U2A=1, and now CLK=1 makes U2B=1. This causes the gate to change state and U2Y goes from 1 to 0. U3 doesn’t do anything however, as while U3B goes to 1, U3C is still 0, as so “blocks” U3 from changing. This gives the following state for all inputs/outputs:

   Gate	A	B	C	Y
   U1	0	0		1
   U2	1	1		0
   U3	0	1	0	1
   U4	1	1		0

8. Thus R=0 and S=1, and the output latch gets “set”.
9. If D changes back from 1 to 0 it will effect the output of U4Y which will go from 0 to 1. However, this output will not effect gates U1 and U3 as they are both now “blocked” from changing because U2Y=0, meaning they both have at least one 0 input.

In Summary

When the CLK transitions from 0 to 1, the output latch gets set if D=1 and gets reset if D=0. Within 1 NAND gate propagation delay, further changes to D do not affect the output as D is now blocked by other 0’s and the inputs to the NAND gates (either immediately by U4 or by U2 and U3). This is the exact behaviour we wanted!

A common example of this style is the Texas Instruments SN7474 “Dual D-Type Positive-Edge Triggered Flip-flops with Reset and Clear”⁵.

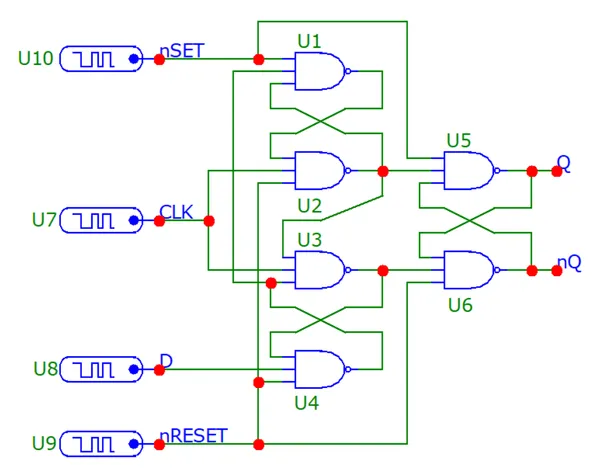
This circuit gets even more complicated when you add asynchronous set and reset inputs! Rather than just the 1 three-input NAND gate, all NAND gates need to be three-input.

Example

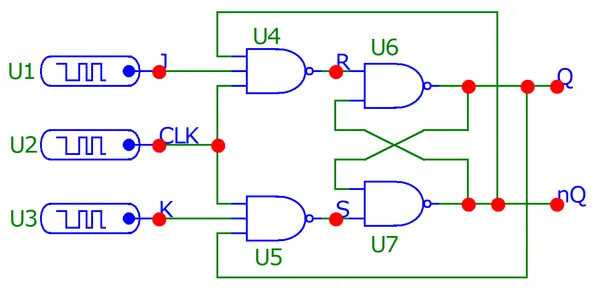
Let’s simulate a NAND-based edge-triggered D-type flip-flop with asynchronous set and reset inputs. The schematic is:

The Micro-Cap schematic for simulating a edge-triggered D-type flip-flop with async. set and reset.

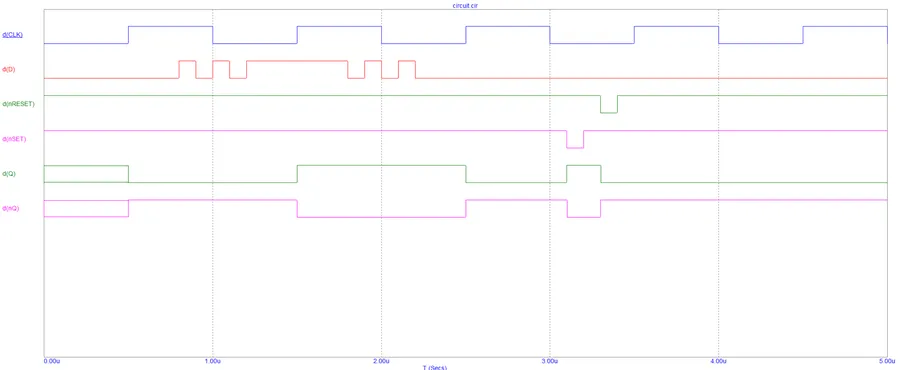
The resulting transient analysis looks as expected! (explanation below graph):

The transient analysis of the above circuit.

Explanation of behaviour:

1. The flip-flop first starts up in an undefined state. We don’t use the nSET or nRESET pins to fix this, we’ll test those later. So the flip-flop output first transitions into a valid state on the transition of the first positive-going clock pulse at 0.5us. Because D=0, Q gets set to 0.
2. D is then “wiggled” back and forth between 0 and 1 and there is no change in the output.
3. The next output transition happens at t=1.5us, when there is another positive clock edge while D=1. Thus Q gets set correctly to 1. Again, no amount of changing D after the edge affects the output.
4. Then we have a play around with the asynchronous reset and set inputs. At t=3.1us, we drive nSET low, which correctly sets Q high, regardless of the clock. Then at t=3.3us we drive nRESET low and it correctly sets Q back to 0, again, asynchronous to the clock.
5. Everything looks like it is working correctly!

The Micro-Cap circuit file used to perform this simulation can be downloaded here.

You can play around with the interactive D flip-flop simulation below. Toggle the level of the data line by clicking on the H, and watch the output only change on the positive edge of the clock!

(full page version)

A D-type flip-flop made from 6 NAND gates (1 being a 3-input NAND gate), with each NAND gate being made from discrete P (Microchip VP2106N3-G) and N-channel (onsemi 2N7000-D75Z) MOSFETs (i.e. CMOS technology) in the TO-92 package. Everything was powered from a +5V rail. This goes to show you how many transistors are needed even for simple things such as a D flip-flop!

D-Type Flip-Flops with Transmission Gates

In reality, the actual D-type flip-flops you can buy can be much more complicated than what we have just discussed! This is the logic diagram for the Nexperia 74HC74 dual D-type flip-flop IC⁶:

Logic diagram for 1 of the positive-edge triggered D-type flip-flops in the Nexperia 74HC74 IC. Note the complexity!⁶

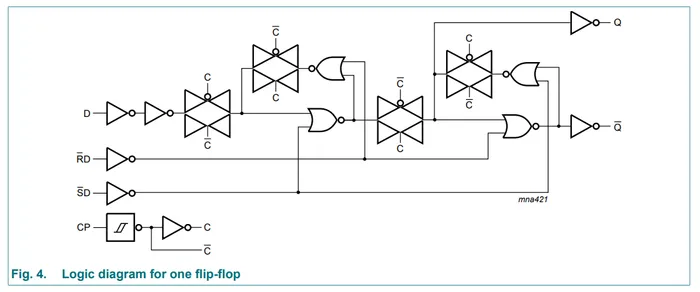
The four triangles pointing towards each other are transmission gates (TGs), normally made from one N-channel and one P-channel MOSFET connected in parallel (with the substrate not connected to the body, to avoid conduction through it’s internal diodes). Some of the circuitry that seems to serve no purpose (like the two inverters in series on the D input) has been presumably added to balance propagation times.

Examples

The partial part number 74HC74 is a dual D-type CMOS positive-edge triggered flip-flop with set and reset. It has balanced propagation delays. Orderable variants include the Nexperia 74HC74D and Toshiba 74HC74D.

Going from the 74 above to the 174 gives you an Hex (6 units) D-type flip-flop IC with reset. It has a shared CLK and reset line. One such example is the Texas Instruments CD74HC174.

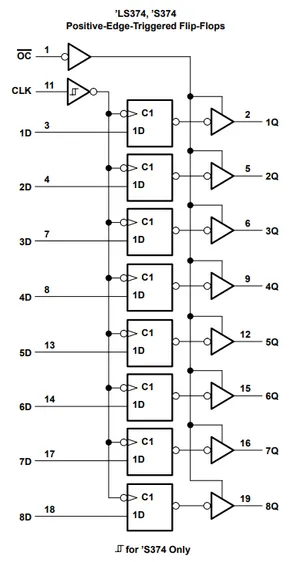
The partial part number LS734 is used for an 8-channel (octal) edge-triggered D-type flip-flop IC. The Texas Instruments 74LS373 is one such example.

Logic diagram of the Texas Instruments 74LS373 Edge-Triggered D-type Flip-flop IC⁷.

Triggering

Edge-triggered D flip-flops can be either positive or negative edge triggered. Edge-triggered flip-flops are shown by a triangle at the clock input, and negative edge-triggered ones have an additional bubble. However, positive-edge triggered is much more common, and standard practice is to make a negative edge triggered flip-flop by adding your own inverting gate on the clock signal.

Note

Adding an inverting gate to the clock signal increases the propagation delay for that clock input, and will have a significant impact on the operation in high-speed designs.

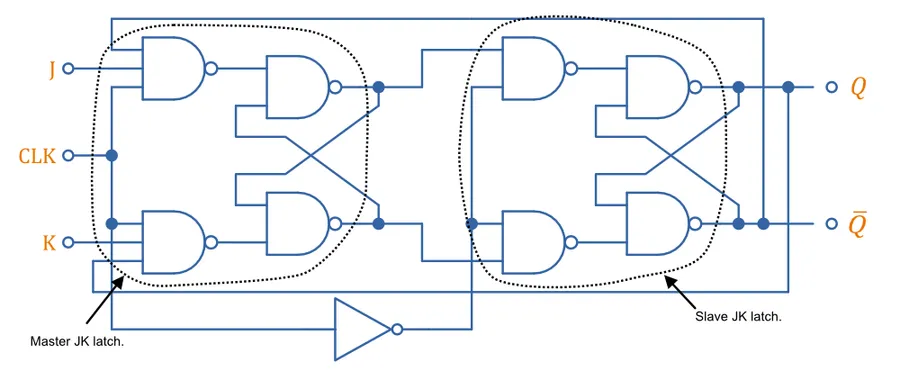
Master-Slave JK Flip-Flop

In a similar manner to the master-slave D flip-flop above, a master-slave JK flip-flop is made from connecting two JK latches in series. Sometimes the “master-slave” part of it’s name is dropped and this circuit is just called the JK flip-flop.

The construction of a master-slave JK flip-flop.

It behaves in the same manner as a JK latch, but only acts on the negative clock-edge. Here is the truth table for this NAND-gate based master-slave JK flipflop:

Inputs			Outputs		Action
CLK	J	K	$Q_{n+1}$	$\overline{Q_{n+1}}$
↓	0	0	$Q$	$\overline{Q}$	No change
↓	0	1	0	1	Reset
↓	1	0	1	0	Set
↓	1	1	$\overline{Q}$	$Q$	Toggle

↓ represents the falling edge of the clock. All states for the clock except for the negative-edge (i.e. rising edge, high level, low level) do not cause any change.

You can play around with the interactive simulation below:

(full page version)

Timing Requirements

Setup and Hold Times

Synchronous flip-flops have timing requirements that must be obeyed. The two main requirements are:

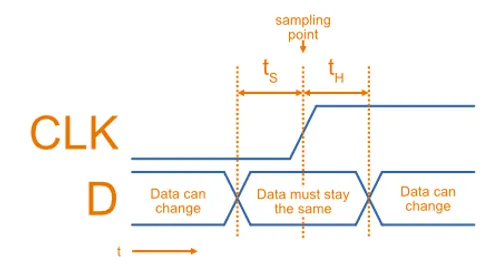
• Setup time $t_S$: This is the time that the data line must be stable for BEFORE the edge of the clock signal.
• Hold time $t_H$: This is the time that the data line must be stable for AFTER the edge of the clock signal.

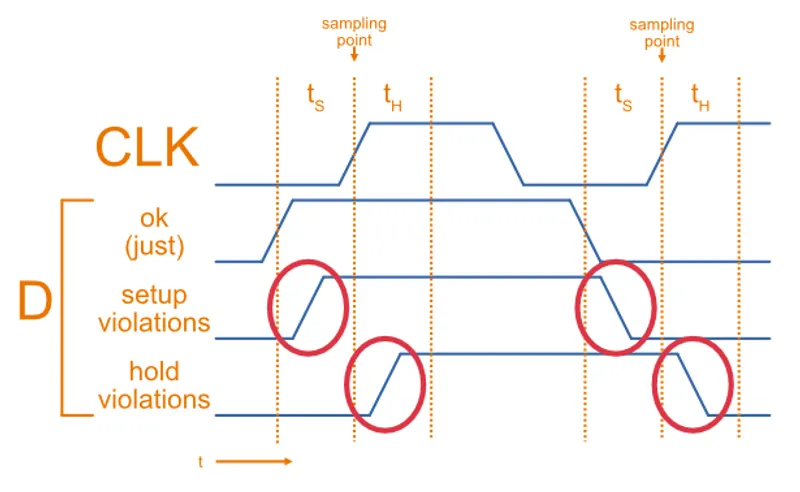
The below diagram shows this concept, assuming the logic is triggered on the positive-edge of the clock signal.

Diagram showing how the setup and hold time are defined.

The edges of the signals have been drawn at a diagonal to illustrate that the signals do not instantly change state, and that the setup and hold times are defined from when the signal voltage passes through the half-way point between LOW and HIGH. In reality, the edges may not be straight lines but feature somewhat of an exponential curve due to capacitance.

What do violating signals look like? Violating signals is when the data signal changes state in the setup or hold period, as illustrated in the diagram below.

Diagram illustrating the concept of setup and hold times, and showing 3 different data signals, one which is just ok, one which violates the setup time requirement and one which violates the hold time requirement.

Recovery and Removal Times

A similar but different concept to setup and hold times are recovery and removal times. Recovery and removal times are terms used to describe the timing requirements for edge-triggered logic for when asynchronous inputs (like set and reset) are de-asserted and the next clock edge⁸.

When set or reset are ASSERTED, there are no timing requirements since the action is asynchronous. The output of the flip-flop will get set or reset independent of the clock. However, when the set or reset is DE-ASSERTED, it’s not until the next clock edge that the flip-flop removes itself from the effects of set/reset and it’s output $Q$ begins to follow $D$ again. This is where the recovery and removal time requirements come into play:

• Recovery time: The amount of time that the set/clear must stay de-asserted for BEFORE the clock edge.
• Removal time: The amount of time that the set/clear must stay de-asserted for AFTER the clock edge.

If both of these requirements are met, the flip-flop is guaranteed to come out of set or reset on that clock edge. If not, the flip-flop may encounter metastability.

Tip

Recovery and removal time have very similar definitions to setup and hold times, but are applied to the de-assertion of signals to asynchronous inputs like set and reset.

Metastability

Metastability is the problem when digital logic persists for some unbounded amount of time in an invalid state. Metastability can cause glitches, the entirely wrong state, or invalid logic levels to propagate through digital logic systems.

Metastability can arise whenever a signal is sampled close to a transition, leading to indecision as to its correct value. — Montek Singh (UNC Chapel Hill) and Luciano Lavagno (Politecnico di Torino)⁹.

Metastability can occur under the following conditions:

• Digital circuits like edge-triggered D-type flip-flops require the input to be stable for some period before the clock edge (setup time) and some time after the clock edge (hold time) before it is allowed to change. If the input violates these timing conditions the flip-flop may encounter metastability.
• Asynchronous inputs arriving into a synchronous system. In this situation, you cannot totally eliminate the chance of metastability. The best you can do is to add synchronizers to the inputs to make the probability of metastability acceptably small¹⁰.
• When transferring data between two or more different clock domains (groups of circuitry running off different clocks).

Tip

One way to think about the flip-flop setup and hold times is that the flip-flop always has to decide what changed first, the input or the clock signal. The setup and hold makes it obvious to the flip-flop that the input changed before the clock signal. However, if you violate these rules, and the input and clock changes get closer and closer together, it get’s harder and harder for the flip-flop to determine what happened first. This makes it more and more likely that the flip-flop will have trouble determining the output and metastability will likely occur.

Another key principle is that metastability occurs for an unbounded amount of time. That’s another way of saying there is no known upper limit to how long the metastability will take to resolve itself. You might think that this is very bad for any type of circuit. The good news is that the probability of the metastability occurring for longer and longer period falls with an exponential decay¹⁰.

Circuits Built From Latches And Flip-Flops

Toggle Flip-Flop

A toggle flip-flop can be made from an edge-triggered D-type flip-flop with it’s nQ connected to it’s D. The input signal is fed to the CLK.

A toggle flip-flop made from an edge-triggered D-type flip-flop with it’s nQ output connected to it’s D input. The input signal is fed to it’s CLK.

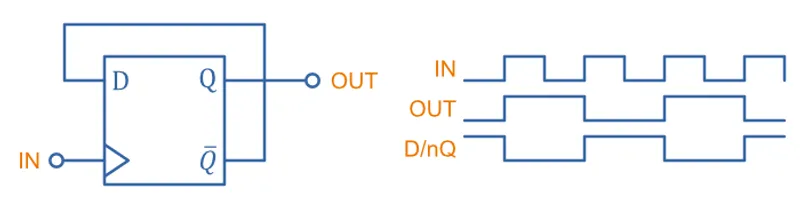
As you can see from the above timing diagram, the output toggles between high and low on every positive clock edge. This also can be considered a divide-by-two device (i.e. the output signal is half the frequency of the input), and is the basis for many digital counters¹¹. Many of these could be connected in series, with the output of the first (Q) being connected to the input of the second (CLK). This would form a simple n-bit digital counter where n is the number of flip-flops in series.

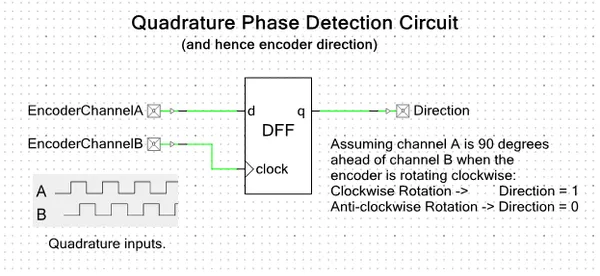
Quadrature Detection Circuit

This quadrature detection circuit is built entirely in hardware, and only uses one flip-flop. It is useful for detecting the direction that an encoder that outputs quadrature signals is spinning in. Potential applications include BLDC motor control. This circuit can be built entirely in reconfigurable PSoC on-chip logic.

When the encoder is spinning in one direction, the output will be logic high (1), when it is spinning in the opposite direction, it will be logic low (0).

A simple quadrature phase detection circuit using a D flip-flop.

Delay Circuit

A simple delay circuit can be made just by chaining DQ flip-flops together in series (the output of one feeds the input of another). For every flip-flop, the signal will be delayed by one clock-cycle (assuming they all share the same clock source).

A simple four clock-cycle delay element made from four DQ flip-flops. This can be used as a simple timer.

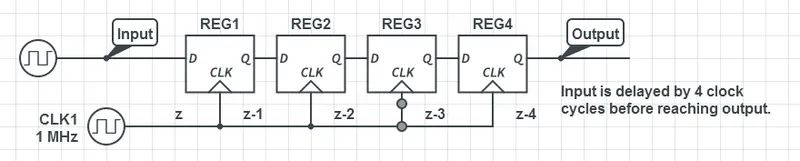
This can be used to make a simple timer. Obviously, a limitation is that a flip-flop is needed for every clock cycle of delay needed (try that with a 1000 clock cycle delay!). More advanced timers use binary encoding with the flip-flops to achieve a greater number of states for a lower number of flip-flops.

Footnotes

1. Texas Instruments (2003, Oct). CD4042B Types: CMOS Quad Clocked “D” Latch. Retrieved 2023-04-22, from https://www.ti.com/lit/ds/symlink/cd4042b.pdf. ↩

2. Priyanshu Vaish (2022, Aug 26). SR Flip-Flop: What is SR Flip-Flop Truth Table?. Byju’s Exam Prep. Retrieved 2023-04-14, from https://byjusexamprep.com/sr-flip-flop-truth-table-i. ↩

3. Electronics Tutorials. The JK Flip Flop. Retrieved 2023-04-14, from https://www.electronics-tutorials.ws/sequential/seq_2.html. ↩

4. Charles W. Kann (2021, May 28). Book: Digital Circuit Projects - An Overview of Digital Circuits Through Implementing Integrated Circuits (Kahn). 9.4: Edge Triggered Flip-Flop. LibreTexts: Engineering. Retrieved 2023-04-11 from https://eng.libretexts.org/Bookshelves/Electrical_Engineering/Electronics/Book%3A_Digital_Circuit_Projects_-_An_Overview_of_Digital_Circuits_Through_Implementing_Integrated_Circuits_(Kahn)/09%3A_Memory_Basics_-_Flip-Flops_and_Latches/9.04%3A_Edge_Triggered_Flip-Flop#:~:text=It%20is%20said%20to%20trigger,will%20be%20positive%20edge%20trigger. ↩

5. Texas Instruments (1988, March). SN5474, SN54LS74A, SN54S74, SN7474, SN74LS74A, SN74S74 - Dual D-Type Positive-Edge Triggered Flip-Flops With Preset And Clear. Retrieved 2023-04-12 from https://www.ti.com/lit/ds/symlink/sn54ls74a-sp.pdf. ↩ ↩²

6. Nexperia (2023, Feb 9). 74HC74; 74HCT74 - Dual D-type flip-flop with set and reset; positive edge-trigger. Retrieved 2023-04-11 from https://assets.nexperia.com/documents/data-sheet/74HC_HCT74.pdf. ↩ ↩²

7. Texas Instruments (2002, Aug). SN54LS373, SN54LS374, SN54S373, SN54S374, SN74LS373, SN74LS374, SN74S373, SN74S374 Octal D-type Transparent Latches and Edge-triggered Flip-flops. Retrieved 2023-04-12 from https://www.ti.com/lit/ds/symlink/sn54ls373-sp.pdf. ↩

8. VLSI Universe. Recovery and removal checks. Retrieved 2023-04-24, from https://vlsiuniverse.blogspot.com/2017/04/recovery-and-removal-checks.html. ↩

9. Ran Ginosar (2011, Oct). Metastability and Synchronizers: A Tutorial. IEEE CS/CASS. Retrieved 2023-04-23, from https://webee.technion.ac.il/~ran/papers/Metastability-and-Synchronizers.IEEEDToct2011.pdf. ↩

10. Wikipedia (2022, Nov 2). Metastability (electronics). Retrieved 2023-04-23, from https://en.wikipedia.org/wiki/Metastability_(electronics). ↩ ↩²

11. Eric Coates (2020, 29th Dec). Module 5.3: D Type Flip-flops. Learn about electronics. Retrieved 2023-04-18, from https://learnabout-electronics.org/Digital/dig53.php. ↩