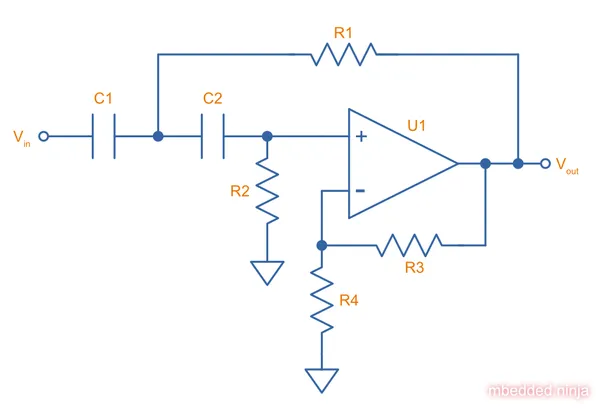
Sallen-Key Filters

The Sallen-Key filter is one of the most popular active 2nd-order analogue filters topologies¹. It can be configured as a low-pass, high-pass, band-pass or band-stop filter. Also called a Sallen and Key filter. It was first introduced in 1955 by R.P. Sallen and E.L. Key of MIT’s Lincoln Labs, whose last names give this filter it’s name. It is a filter topology, and defines the components and connections between them to realize a 2nd order filter. Various filter tunings such as Butterworth, Bessel and Chebyshev can be implemented using the Sallen-Key topology.

The schematic for a variable-gain low-pass Sallen-Key filter.

Simulated response of the design example (2nd-order 3dB Chebyshev Sallen-Key low-pass filter with a cutoff frequency of 1kHz) above.

The Sallen-Key filter has low component spread (low ratios of highest to lowest capacitor and resistor values). It also has a high input impedance and low output impedance, allowing for multiple filters to be chained together without intermediary buffers.

The performance of a Sallen-Key filters does not depend that much on the performance of the op-amp. This is because the op-amp is used as an amplifier, rather than an integrator, which minimizes the gain-bandwidth requirements of the op-amp¹. However there are high-frequency limitations to the Sallen-Key filter, which are explained in more detail below.

One disadvantage of the Sallen-Key filter is that the Q of the filter is very sensitive to component variations, which can be a problem, especially for high-Q filter sections.

The Sallen-Key filter is closely related to a voltage-controlled voltage source (VCVS) filter. Some literature makes the distinction of a Sallen-Key filter having unity gain, and the VCVS filter including non-unity gain by connecting a resistor divider from the output to the inverting terminal of the op-amp. However we will consider them one and the same for the purpose of analysis, as the unity-gain version is a special subtype of the generalized variable-gain version.

Another popular alternative to the Sallen-Key topology is the Multiple Feedback (MFB) topology².

Low-Pass Sallen-Key Filter

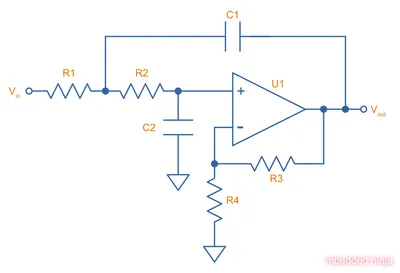
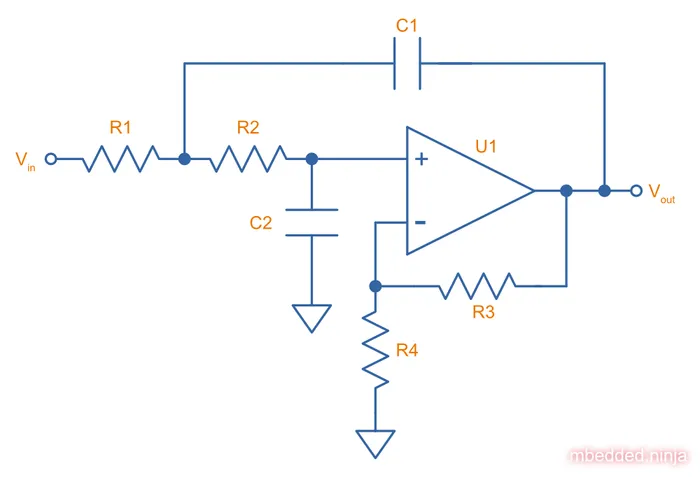
This is a placeholder for the reference: fig-low-pass-variable-gain-sallen-key-filter-schematic shows the schematic for a variable-gain low-pass Sallen-Key filter (a.k.a. VCVS filter).

The schematic for a variable-gain low-pass Sallen-Key filter.

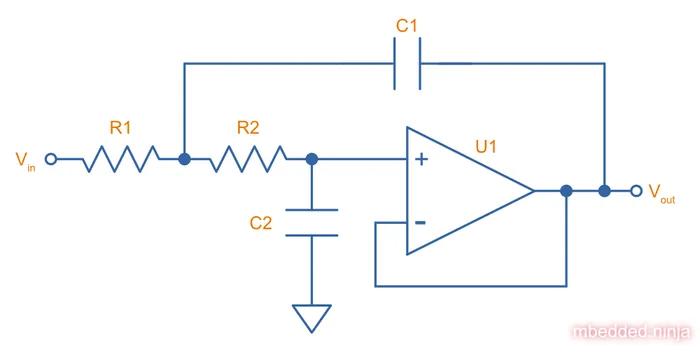
This is a placeholder for the reference: fig-low-pass-unity-gain-sallen-key-filter-schematic shows the schematic for the unity-gain low-pass Sallen-Key filter (which is generally not called a VCVS filter). Note the removal of $R_3$ and $R_4$, the output is instead directly fed into the inverting input of the op-amp, just like when using an op-amp as a buffer. The filter has unity gain in the pass-band.

The schematic for a unity-gain low-pass Sallen-Key filter.

Caution

Take note of labelling of the resistors and capacitors if reading other material on Sallen-Key filters, there is no one popular convention as the resistor and capacitor orders are switched frequently.

The generalized transfer function for a 2nd-order low-pass filter is^{1 3}:

$$\begin{align} H(s) &= \frac{K\omega_0^2}{s^2 + \frac{\omega_0}{Q}s + \omega_0^2} \\ \end{align}$$

where:
$K$ is the gain factor
$\omega_0$ is the characteristic frequency in radians/s [$rads^{-1}$]
$Q$ is the quality factor and is dimensionless [$no\ unit$]
$s = j\omega$

Tip

For any general 2nd-order filter, the characteristic frequency $\omega_0$ is not necessarily equal to the cut-off frequency. Also, $\frac{1}{Q}$ is sometimes written as $\alpha$.

Written in the same form as the general equation above, the transfer function for a 2nd-order low-pass Sallen-Key filter is¹:

$$\begin{align} H(s) &= \frac{\frac{K}{R_1R_2C_1C_2}} {s^2 + \left[(\frac{1}{R_1} + \frac{1}{R_2})\frac{1}{C_1} + \frac{1 - K}{R_2C_2} \right]s + \frac{1}{R_1R_2C_1C_2}} \\ \end{align}$$

Equating the coefficients in the general form ($Eq.\ \ref{eq:gen-2-order-lp}$) with those specific to the Sallen-Key topology ($Eq.\ \ref{eq:sallen-key-2-order-lp}$) allows us to find the equations of the characteristic frequency and quality factor.

The cut-off frequency is (remembering $f = 2\pi \omega$):

$$\begin{align} f_c = \frac{1}{2\pi \sqrt{R_1R_2C_1C_2}} \end{align}$$

and the quality factor is:

$$\begin{align} Q = \frac{\sqrt{R_1R_2C_1C_2}}{R_1C_1 + R_2C_1 + R_1C_2(1 - K)} \end{align}$$

The gain equation is the same as for an non-inverting amplifier:

$$\begin{align} K = 1 + \frac{R_3}{R_4} \end{align}$$

How To Calculate Component Values

Setting Filter Components As Ratios

The idea here is to define a new variable $m$ which is the ratio of the resistances and a new variable $n$ which is a ratio of the capacitances.

So we define:

$$\begin{align} R_1 = mR,\ R_2 = R,\ C_1 = C,\ C_2 = nC \\ \end{align}$$

This simplifies the cut-off frequency and quality factor equations to:

$$\begin{align} f_c &= \frac{1}{2\pi RC\sqrt{mn}} \\ Q &= \frac{\sqrt{mn}}{m + 1 + mn(1 - K)} \\ \end{align}$$

Firstly, you decide on a desired gain $K$ and quality factor $Q$. Then chose a ratio $n$ for the capacitors, for example $1$. This will allow you to calculate $m$ using the equation for the quality factor.

With arbitrary $K$, $Q$ and $n$, solving the quality factor equation for $m$ gives something truly horrible (I cheated and got Wolfram Alpha to solve this one for me):

$$\begin{align} m = \frac{2 K n Q^2 \pm \sqrt{n} \sqrt{4 K n Q^2 - 4 n Q^2 + n - 4 Q^2} - 2 n Q^2 + n - 2 Q^2}{2 Q^2 (K^2 n^2 - 2 K n^2 - 2 K n + n^2 + 2 n + 1)} \end{align}$$

Lastly, decide on your cut-off frequency $f_c$ and then you can calculate $R$ using the cut-off frequency equation.

$$\begin{align} R &= \frac{1}{2\pi f_c C\sqrt{mn}} \\ \end{align}$$

The process can be simplified even more, by setting $n = 1$. This makes both capacitors equal.

Example

Design Example: Low-Pass K=5, Q=1 Sallen-Key Filter Using mn Ratios

Design goals:

• Cut-off frequency $f_c = 10kHz$
• Gain $K = 5$
• Quality factor $Q= 1$

Let’s first calculate the ratios of resistances and capacitances, $m$ and $n$. We get to choose $n$, so let’s go with $n = 1$ to simplify things. Substituting values into the quality factor equation gives us:

$$\begin{align} 1 &= \frac{\sqrt{m}}{-3m + 1} \nonumber \\ \sqrt{m} &= -3m + 1 \nonumber \\ m &= 9m^2 -6m + 1 \nonumber \\ 9m^2 -7m + 1 = 0 \nonumber \\ \end{align}$$

We can use the quadratic equation to find the two solutions for $m$. Only one of them is gives a real number for $m$ since the initial square root forces $m$ to be positive. Thus:

$$\begin{align} m = 0.189 \nonumber \\ \end{align}$$

We have the freedom to choose $C$, and because $n = 1$, $C_1 = C_2 = C$. Let’s choose $C = 10nF$, and therefore:

$$\begin{align} C_1 &= 10nF \nonumber \\ C_2 &= 10nF \nonumber \\ \end{align}$$

Using the cutoff frequency equation, we can now find $R$:

$$\begin{align} R &= \frac{1}{2\pi f_c C\sqrt{mn}} \nonumber \\ &= \frac{1}{2\pi 10kHz \times 10nF \sqrt{0.189}} \nonumber \\ &= 3.66k\Omega \nonumber \\ \end{align}$$

Choosing the closest E96 value for $R_2$, and calculating $R_1$:

$$\begin{align} R_2 &= R \nonumber \\ &= 3.65k\Omega\ (E96) \nonumber \\ R_1 &= mR \nonumber \\ &= 0.189 \times 3.66k\Omega \nonumber \\ &= 692\Omega \nonumber \\ &= 698\Omega\ (E96) \nonumber \\ \end{align}$$

Lastly, we can calculate the values of the gain resistors. Choose a value for $R_4=1k\Omega$. Then using the gain equation we can find $R_3$:

$$\begin{align} K &= 1 + \frac{R_3}{R_4} \nonumber \\ R_3 &= (K - 1)R_4 \nonumber \\ &= (5 - 1) \times 1k\Omega \nonumber \\ &= 4k\Omega \nonumber \\ &= 4.02k\Omega\ (E96) \nonumber \\ \end{align}$$

All done! This is a placeholder for the reference: fig-low-pass-sallen-key-mn-ratios-schematic shows our finished schematic.

The finished schematic of the low-pass Sallen-Key filter designed using the mn ratio technique.

This is a placeholder for the reference: fig-low-pass-sallen-key-mn-ratios-bode-plot shows the simulated frequency and phase response for this circuit.

The simulated bode plots for the low-pass Sallen-Key filter designed using the mn ratio technique.

We chose a $Q$ above 0.707, so we expect some peaking in the gain response around cut-off.

Tuning Based Design

You can design a Sallen-Key filter based of a particular filter tuning and it’s coefficients, this is an alternative to choosing the quality factor and gain yourself. Given the filter tuning coefficients $a_0$ and $a_1$ and desired cut-off frequency $f_c$ you can then calculate the required resistances and capacitances.

The resistance of the resistors $R_1$ and $R_2$ are related to the capacitances and filter coefficients by the following equation:

$$\begin{align} R_1, R_2 = \frac{a_1 C_1 \mp \sqrt{ (a_1 C_1)^2 - 4 b_1 C_1C_2}}{4\pi f_c C_1 C_2} \end{align}$$

You use the $-$ sign when calculating $R_1$ and the $+$ sign for calculating $R_2$.

To obtain real values under the square root, $C_1$ must obey the follow condition:

$$\begin{align} C_1 \geq C_2 \frac{4b_1}{a_1^2} \end{align}$$

Note

The choice of resistances affects the cut-off frequency, but the choice of capacitors does not.

These equations give you enough info to calculate all the resistances and capacitors for a Sallen-Key filter. See the design example below to show how you would go about it.

Example

Design Example: 2nd-Order Low-Pass Unity-Gain 3dB-Chebyshev Sallen-Key Filter

The task is to design a 2nd-order unity-gain Sallen-Key filter optimized with Chebyshev 3dB ripple coefficients (this will give us a sharp transition from the passband to the stopband) and a corner frequency of $f_c = 1kHz$.

1. Look up the Chebyshev filter coefficients. From the table we get:

   $$\begin{align} a_1 = 1.0650 \\ b_1 = 1.9305 \\ \end{align}$$

2. Choose a capacitance for $C_2$. This is rather arbitrary, but a good recommended starting range is something between $1-100nF$. Lets pick:

   $$\begin{align} C_2 = 10nF \end{align}$$

3. Calculate the capacitance of $C_1$:

   $$\begin{align} C_1 &\geq C_2 \frac{4b_1}{a_1^2} \\ &\geq 10nF \frac{4\cdot1.9305}{1.0650^2} \\ &\geq 68.1nF \end{align}$$

   Pick the next largest E12 value:

   $$\begin{align} C_1 = 82nF \end{align}$$

4. Calculate $R_1$ and $R_2$:

   $$\begin{align} R_1 &= \frac{a_1 C_1 - \sqrt{(a_1 C_1)^2 - 4 b_1 C_1C_2}}{4\pi f_c C_1 C_2} \\ &= \frac{1.0650 \cdot 82nF - \sqrt{1.0650^2 \cdot 82nF^2 - 4 \cdot 1.9305 \cdot 10nF \cdot 82nF}}{4\pi \cdot 1kHz \cdot 10nF \cdot 82nF} \\ &= 4.98k\Omega \end{align}$$ $$\begin{align} R_2 &= \frac{a_1 C_2 + \sqrt{a_1^2 C_2^2 - 4 b_1 C_1C_2}}{4\pi f_c C_1 C_2} \\ &= \frac{1.0650 \cdot 82nF + \sqrt{1.0650^2 \cdot 82nF^2 - 4 \cdot 1.9305 \cdot 10nF \cdot 82nF}}{4\pi \cdot 1kHz \cdot 10nF \cdot 82nF} \\ &= 12.0k\Omega \end{align}$$

   Pick the closest E96 values:

   $$\begin{align} R_1 = 4.99k\Omega \\ R_2 = 12.1k\Omega \end{align}$$

5. Build the circuit! It should look like that in This is a placeholder for the reference: fig-low-pass-sallen-key-chebyshev-3db-schematic-print.

Schematic of the design example (2nd-order 3dB Chebyshev Sallen-Key low-pass filter with a cutoff frequency of 1kHz) above.

1. And just good measure this was simulated, to make sure the response is as expected.

Simulated response of the design example (2nd-order 3dB Chebyshev Sallen-Key low-pass filter with a cutoff frequency of 1kHz) above.

Frequency Limitations of the Low-Pass Sallen-Key Filter

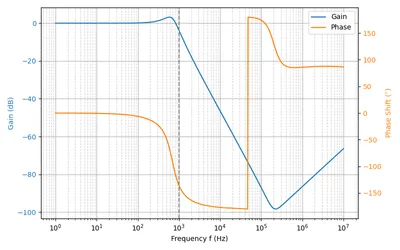
A low-pass Sallen-Key filter is strongly dependent on the op-amp having a low output impedance. A op-amp’s output impedance increases with increasing frequency, thus the performance of the Sallen-Key low-pass begins to suffer at high frequencies. This typically manifests itself with the -40dB/decade gain turning around and beginning to increase again after a certain frequency in the stop band of the filter.

This phenomenon can be best understood by analyzing the behaviour at high frequencies. At frequencies much higher than the cut-off frequency $f_c$, we can treat the capacitors as shorts. This gives rise to the equivalent circuit in This is a placeholder for the reference: fig-low-pass-variable-gain-sallen-key-filter-freq-limit. Shorting $C_2$ means that the op-amps non-inverting input is kept at ground (for high frequency signals), and so nothing should pass from input to output. This is true as long as the op-amp has strong enough “drive” to keep this basic tenant true. Unfortunately, as frequency increases, so does the op-amps output impedance. This impedance effects the op-amps ability to keep the output at $0V$, and the gain begins to rise again.

Equivalent circuit for a low-pass Sallen-Key filter at high frequencies. The left-hand shows the circuit with the capacitors shorted. The right-hand is a simplification showing the addition of the op-amps output impedance.

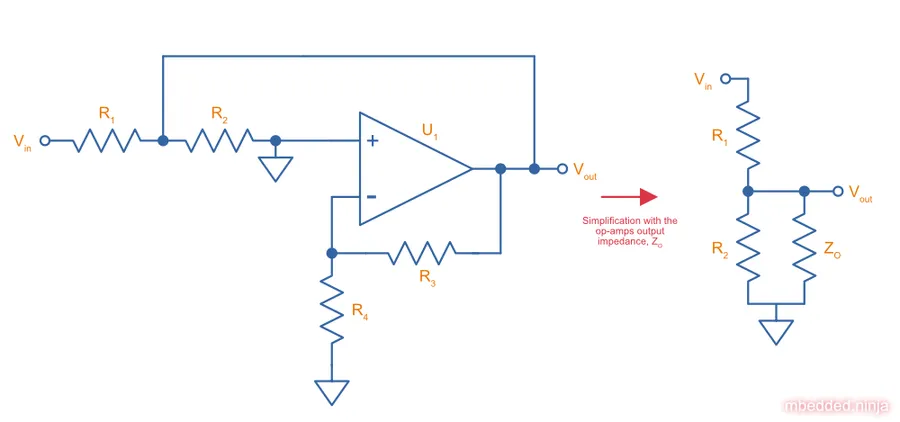
Based of the above schematic, we can use the voltage divider rule to write out the transfer function as:

$$\begin{align} \frac{V_{out}}{V_{in}} &= \frac{R_2 || Z_O}{R_1 + R_2 || Z_O} \nonumber \\ &= \frac{1}{\frac{R_1}{R_2 || Z_O} + 1} \nonumber \\ &= \dfrac{1}{\dfrac{R_1}{\frac{R_2Z_O}{R_2 + Z_O}} + 1} \nonumber \\ &= \dfrac{1}{\frac{R_1(R_2 + Z_O)}{R_2Z_O} + 1} \nonumber \\ &= \dfrac{1}{\frac{R_1R_2 + R_1Z_O}{R_2Z_O} + 1} \nonumber \\ &= \dfrac{1}{\frac{R_1}{Z_O} + \frac{R_1}{R_2} + 1} \\ \end{align}$$

Assuming $Z_O$ is much smaller that $R_1$, and that $R_1$ and $R_2$ are roughly in the same order of magnitude, the $\frac{R_1}{Z_O}$ term then dominates the bottom of the fraction. Thus:

$$\begin{align} \frac{V_{out}}{V_{in}} &\approx \frac{Z_O}{R_1} \\ \end{align}$$

$Z_O$ is the closed-loop impedance. It is frequency-dependent, and is related to the open-loop impedance by:

$$\begin{align} Z_O = \frac{z_O}{1 + AB} \\ \end{align}$$

where:
$z_O$ is the open-loop impedance
$A$ is the closed-loop gain
$B$ is the feedback factor, and equal to $\frac{R_4}{R_3 + R_4}$

So as the closed-loop gain $A$ of the op-amp begins to drop at high frequencies, the output impedance of the op-amp begins to increase. The op-amp then struggles to keep the inverting input of the low-pass Sallen-Key filter at virtual ground, and begins to let through some of the signal. This reduces the effectiveness of the low-pass filter in the stop band.

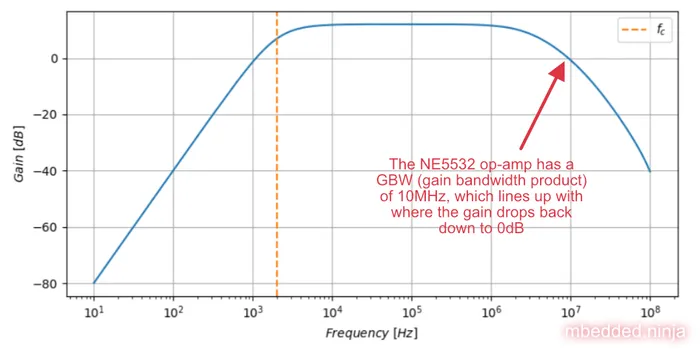
We can see the effect of an increasing output impedance at high frequencies in bode plot of This is a placeholder for the reference: fig-low-pass-sallen-key-showing-gain-rise-annotated-plot for a 2nd-order low-pass Sallen-Key filter, with a cutoff frequency $f_c$ of 1kHz.

Gain plot of a low-pass Sallen-Key filter showing the reversal to increasing again once a certain frequency is reached, owing to the increasing op-amp output impedance.

High-Pass Sallen-Key Filter

You can arrive at a high-pass Sallen-Key filter by switching the positions of the resistors and capacitors in a low-pass Sallen-Key filter (just like you can for passive RC filters). This gives you the schematic in This is a placeholder for the reference: fig-high-pass-variable-gain-sallen-key-filter-schematic.

Schematic of a variable-gain high-pass Sallen-Key filter.

The general form of the transfer function for a second order high-pass filter is¹:

$$\begin{align} H(s) = \frac{Ks^2}{s^2 + \alpha \omega_0 s + \omega_0^2} \\ \end{align}$$

Using Ohm’s law and Kirchhoff’s current/voltage laws, we can write the equivalent transfer function for a variable-gain high-pass Sallen-Key filter, in terms of the resistances and capacitances¹:

$$\begin{align} H(s) &= \frac{Ks^2}{s^2 + \left( \dfrac{\frac{C_2}{R_2} + \frac{C_1}{R_2} + (1-K)\frac{C_2}{R_1}}{C_1C_2} \right)s + \dfrac{1}{R_1C_1R_2C_2}} \\ \end{align}$$

If you are using the unity-gain op-amp (no $R_3$ or $R_4$), the transfer function simplifies to⁴:

$$\begin{align} H(s) &= \frac{s^2}{s^2 + \left(\dfrac{1}{R_2C_1} + \dfrac{1}{R_2C_2}\right)s + \dfrac{1}{R_1C_1R_2C_2}} \\ \end{align}$$

This unity-gain transfer function is similar to the unity-gain transfer function for the low-pass filter, except note:

1. It’s just $s^2$ on the numerator.
2. The coefficient for $s$ on the denominator changes from $\left(\frac{1}{R_1C_1} + \frac{1}{R_2C_2}\right)$ to $\left(\frac{1}{R_2C_1} + \frac{1}{R_2C_2}\right)$.

This means our unity-gain filter coefficients $a_0$ and $a_1$ are:

$$\begin{align} a_0 &= \frac{1}{R_1 \times R_2 \times C_1 \times C_2} \\ a_1 &= \frac{1}{R_2 \times C_1} + \frac{1}{R_2 \times C_2} \\ \end{align}$$

How To Calculate Component Values

This design process assumes the following inputs:

• Cut-off frequency $f_c$
• Quality factor $Q$
• Gain $K$

This process is based of Basic Linear Design: Chapter 8 - Page 8.90.

Choose $C_1$. Set $C_2$ to the same value.

Then calculate an intermediary variable $k$, with:

$$\begin{align} k = 2\pi f_c C_1 \\ \end{align}$$

Caution

Make sure not to confuse this intermediary variable $k$ with the gain $K$.

Find $\alpha$, which by definition is the inverse of the quality factor:

$$\begin{align} \alpha = \frac{1}{Q} \\ \end{align}$$

$R_1$ and $R_2$ are then:

$$\begin{align} R_1 &= \frac{\alpha + \sqrt{\alpha^2 + (K - 1)}}{4k} \\ R_2 &= \frac{4}{\alpha + \sqrt{\alpha^2 + (K - 1)}} \times \frac{1}{k} \\ \end{align}$$

Example

Design Example: High-Pass Sallen-Key Filter With fc=2kHz, Q=0.8, K=4

Inputs:

• Cut-off frequency of $f_c = 2kHz$
• Quality factor of $Q = 0.8$
• Pass-band gain of $K=4$

1. Firstly, choose the two capacitances to be equal and within a sensible range. $C_1 = C_2 = 10nF$.

2. Calculate the intermediary $k$ variable:

   $$\begin{align} k &= 2\pi f_c C_1 \nonumber \\ &= 2\pi \times 2kHz \times 10nF \nonumber \\ &= 1.26\times 10^{-4} \nonumber \\ \end{align}$$

3. Calculate $\alpha$:

   $$\begin{align} \alpha &= \frac{1}{Q} \nonumber \\ &= \frac{1}{0.8} \nonumber \\ &= 1.25 \nonumber \\ \end{align}$$

4. Calculate $R_1$ and $R_2$:

   $$\begin{align} R_1 &= \frac{\alpha + \sqrt{\alpha^2 + (K - 1)}}{4k} \nonumber \\ &= \frac{1.25 + \sqrt{1.25^2 + (4 - 1)}}{4\times 1.26\times 10^{-4}} \nonumber \\ &= 6.74k\Omega \nonumber \\ &= 6.81k\Omega\ (E96) \nonumber \\ R_2 &= \frac{4}{\alpha + \sqrt{\alpha^2 + (K - 1)}} \times \frac{1}{k} \nonumber \\ &= \frac{4}{1.25 + \sqrt{1.25^2 + (4 - 1)}} \times \frac{1}{1.26\times 10^{-4}} \nonumber \\ &= 9.40k\Omega \nonumber \\ &= 9.31k\Omega\ (E96) \nonumber \\ \end{align}$$

5. Choose $R_4 = 1k\Omega$. Then calculate $R_3$:

   $$\begin{align} R_3 &= R_4 (K - 1) \nonumber \\ &= 1k\Omega (4 - 1) \nonumber \\ &= 3k\Omega \nonumber \\ &= 3.01k\Omega\ (E96) \nonumber \\ \end{align}$$

6. Done! The finished schematic ready for simulating is shown in This is a placeholder for the reference: fig-high-pass-sallen-key-fc2khz-q1.5-k4-schematic.

   

   The simulation-ready schematic of our 2kHz high-pass Sallen-Key filter.

   And the simulated bode plot in This is a placeholder for the reference: fig-high-pass-sallen-key-fc2khz-q1.5-k4-bode-plot.

   

   The simulation-ready schematic of our 2kHz high-pass Sallen-Key filter.

Frequency Limitations of the High-Pass Sallen-Key Filter

The high-pass Sallen-Key filter works well up to a certain frequency, and after which the non-idealities of the op-amp begin to reduce the gain. This turns the high-pass Sallen-Key filter more into a band-pass filter, with the upper frequency cut-off determined by the open-loop gain of the op-amp.

At frequencies much higher than the cut-off $f_c$, we can assume the two capacitors are shorts. This gives us the schematic in This is a placeholder for the reference: fig-high-pass-variable-gain-sallen-key-filter-freq-limit.

Equivalent circuit for high frequency signals through the high-pass Sallen-Key filter. Both capacitors are considered shorts.

Note

Recognize this schematic? It’s essentially a basic non-inverting amplifier! You can somewhat ignore $R_1$ and $R_2$ as they don’t change the basic behaviour of the circuit.

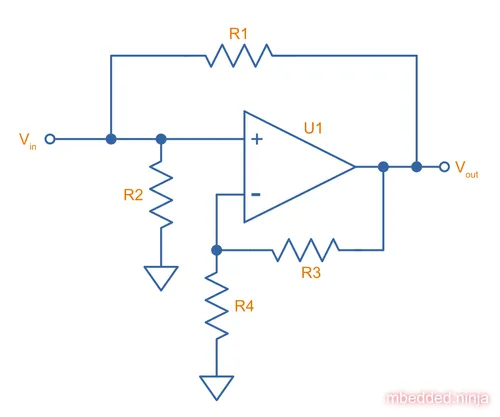
If we assume a non-infinite open-loop gain $A$ of the op-amp, the transfer function of this above circuit is:

$$\begin{align} H(f) &= \frac{A}{AB + 1} \\ \end{align}$$

where $B$ is the feedback factor (how much of the output is fed back to the inverting terminal via the voltage divider made from $R_3$ and $R_4$):

$$\begin{align} B &= \frac{R_4}{R_3 + R_4} \\ \end{align}$$

If we divide the numerator and denominator of $Eq.\ \ref{eq:transfer-fn-high-pass-freq-limit}$ by $AB$ the behaviour of the transfer function as $A$ drops becomes more apparent:

$$\begin{align} H(f) &= \frac{1}{B} \left[\frac{1}{1 + \frac{1}{AB}}\right] \\ \end{align}$$

When the open-loop gain $A$ is large, this equation just becomes $H(f) = \frac{1}{B}$, the standard gain equation for a non-inverting op-amp. However, as $A$ decreases we can no longer ignore the $\frac{1}{AB}$ term and it starts reducing the overall gain of the circuit.

You can a practical example of this frequency limitation with the high-pass Sallen-Key filter we designed above. As shown in This is a placeholder for the reference: fig-high-pass-sallen-key-fc2khz-q1.5-k4-freq-limitation-plot, the gain of the high-pass filter starts falling and hits $0\,dB$ at the stated gain bandwidth product $GBW$ at $10\,MHz$.

Annotated bode plot showing how the upper frequency limit of the high-pass Sallen-Key filter lines up nicely with the stated GBW=10MHz of the op-amp.

Calculators

The OKAWA Electric Design website has some good Sallen-Key filter calculators, including 2nd and 3rd-order low-pass and high-pass calculators.

Screenshot of the Sallen-Key filter calculators offered by the OKAWA Electric Design website⁵.

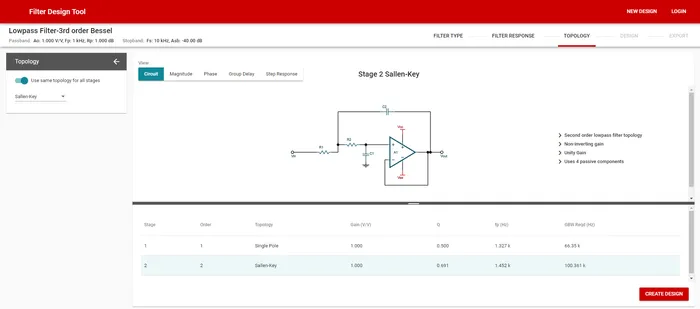
The Texas Instruments Filter Design Tool is a web-based tool that supports the Sallen-Key topology. You firstly enter in the desired characteristics of your filter (e.g. low-pass, cut-off frequency, amount of rejection in stop band, tuning, e.t.c) and then can select Sallen-Key as a topology to implement the filter with.

Screenshot of the Filter Design Tool from Texas Instruments⁶.

Further Reading

For general information on analogue filters, see the Analogue Filters page.

See the Filter Tunings page for information on Butterworth, Bessel, Chebyshev, e.t.c filter tunings and their polynomial coefficients (these can be applied to a Sallen-Key filter topology).

A screenshot of the Filter Tunings page.

Footnotes

1. Analog Devices. Chapter 8: Analog Filters. Retrieved 2022-09-20, https://www.analog.com/media/en/training-seminars/design-handbooks/Basic-Linear-Design/Chapter8.pdf. ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

2. Jim Karki (2002, Sep). SLOA049B: Active Low-Pass Filter Design. Texas Instruments. Retrieved 2022-09-21, from https://www.ti.com/lit/an/sloa049b/sloa049b.pdf. ↩

3. Gary Tuttle. EE 230: Second-order Filters (lecture slides). Retrieved 2022-10-01, from http://tuttle.merc.iastate.edu/ee230/topics/filters/second_order_intro.pdf. ↩

4. Texas Instruments (2021, Jun). SBOA225: Single-supply, 2nd-order, Sallen-Key high-pass filter circuit. Retrieved 2022-09-21, from https://www.ti.com/lit/an/sboa225/sboa225.pdf. ↩

5. OKAWA Electric Design. Filter Design and Analysis (web application). Retrieved 2022-09-29, from http://sim.okawa-denshi.jp/en/Fkeisan.htm. ↩

6. Texas Instruments. Filter Design Tool (web application). Retrieved 2022-09-29, from https://webench.ti.com/filter-design-tool/filter-type. ↩