Linear Programming

Overview

This page provides an introduction to linear programming, with examples which use GNU Linear Programming Toolkit C API.

An example of linear programming with 2 variables. Image from www.wikipedia.com.

What Is Linear Programming Good For?

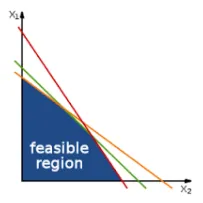
Linear programming is good for **solving problems in the below form:

$$maximise \\ z = 3x_1 + 4x_2 + 7x_3 \\ subject to \\ x_1 + x_2 + x_3 <= 10 \\ x_2 - 5x_3 =5$$

The objective function is the function we want to either maximise or minimise. In the above example, this is:

$z = 3x_1 + 4x_2 + 7x_3$

$z$ is the value we want to maximise, and it is dependent on $x_1, x_2, ...$. The constraints are the equations which the solution is “subject to”. These are the following lines:

$$x_1 + x_2 + x_3 <= 10 \\ x_2 - 5x_3 = 5$$

These limit the values of $x_1, x_2, ...$. You can also have bounds for these variables, such as:

$$10 < x_1 >= 30$$

However, these bounds are just another way of writing a constraint. In fact, the above bound can be written in constraint equation form as:

$$x_1 > 10 \\ x_1 <= 30$$

GLPK

Building GLPK

The GLPK source code can be downloaded from https://www.gnu.org/software/glpk/. This then has to be compiled/built for your computer.

Solving The Example In GLPK

GLPK can either (where the structural variables, x1, x2, … are allowed to vary continuously) or perform mixed-integer programming, where the structural variables must take on a integer number. A sub-set of mixed-integer programming is binary programming, where the structural variables are only allowed to be the integers 0 or 1.

Silencing GLPK

By default, glpk prints a small amount of information to the terminal when the solver is run. To silence this, call:

glp_term_out(GLP_OFF);