Triangles

Triangle geometry pops up time and time again in engineering, in all sorts of things such as robotics, motors, linkages, maps, and sensing (e.g. GPS or ultrasound). It’s helpful to know how to work with triangles and solve for things like unknown side lengths and angles, areas, e.t.c.

This page will teach you how! If you have a right-angles triangle and what to calculate unknown edge lengths or angles, use the basic trigonometric ratios (SOH CAH TOA). If you have a non-right angled triangle (an oblique triangle) but want to also want to solve for lengths and/or angles, use the Law of Sines and/or Law of Cosines.

Trigonometric Ratios

Trigonometric ratios are the three ratios $\sin$, $\cos$, and $\tan$ which are defined using properties of a right-angled triangle (a triangle in which one of the internal angles is $90^{\circ}$). They are useful for solving for unknown side lengths and angles of right-angled triangles, but they also crop up many other situations such as Fourier Series, AC voltage/current, complex numbers (e.g. Euler’s formula) and oscillators.

The Equations

Given you have a triangle with a right-angle in it, and another angle $A$, then the image below shows the naming of the triangle’s sides when using trigonometric ratios.

Diagram illustrating the naming of the triangles sides w.r.t. to angle A when using trigonometric ratios.

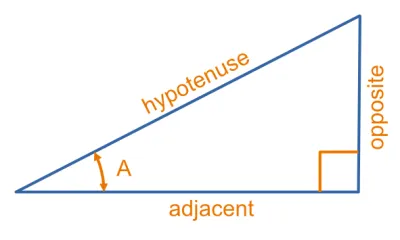
It might be obvious from the figure, but the names are because:

• The hypotenuse is the longest side of the right-angled triangle (it is always opposite the right-angle).
• The opposite side is the side opposite angle $A$.
• The adjacent side if the side next to angle $A$ (but not the hypotenuse).

Using these names, then the trigonometric ratios $\sin$, $\cos$, and $\tan$ are defined as:

$$\begin{align} \sin A &= \frac{\text{opposite}}{\text{hypotenuse}} \\ \cos A &= \frac{\text{adjacent}}{\text{hypotenuse}} \\ \tan A &= \frac{\text{opposite}}{\text{adjacent}} \\ \end{align}$$

There are normally just shortened to:

$$\begin{align} \sin A &= \frac{O}{H} \\ \cos A &= \frac{A}{H} \\ \tan A &= \frac{O}{A} \\ \end{align}$$

Using The sin Ratio

Given the triangle in the image below, calculate the value of angle $A$.

Diagram for the worked example using sin().

Relative to angle $A$, we know the value of the opposite side and the hypotenuse. Thus we need to use the $\sin()$ ratio:

$$\begin{align} \sin A &= \frac{O}{H} \\ \end{align}$$

Re-arrange to solve for $A$:

$$\begin{align} A &= \sin^{-1}\left(\frac{O}{H}\right) \\ \end{align}$$

Plug in the values and solve:

$$\begin{align} A &= \sin^{-1}\left(\frac{O}{H}\right) \\ &= \sin^{-1}\left(\frac{22\text{mm}}{48\text{mm}}\right) \\ &= 27.3^{\circ} \\ \end{align}$$

Tip

$\sin^{-1}()$ is not $\frac{1}{\sin()}$, but rather the inverse of the $\sin$ function. If $\sin(x) = y$, then $\sin^{-1}(y) = x$. This is also called $asin()$ or $arcsin()$ in calculators and programming languages.

Using The tan Ratio

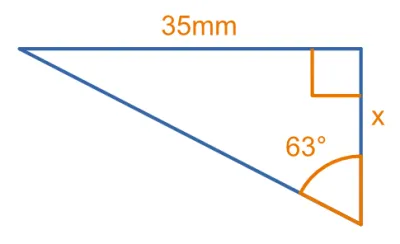
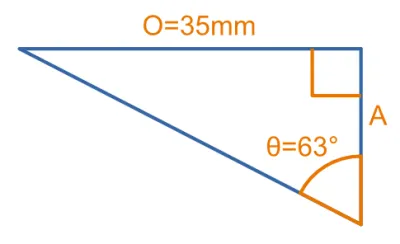
Given the triangle in image below, calculate the length of side $x$.

Diagram for the worked example using tan().

Relative to the known angle, we know the value of the opposite side and want to know the length of the adjacent side. The image below shows the values labelled accordingly.

Triangle now has labelled edges and angles.

The $\tan()$ ratio allows us to use the 2 knowns to solve for the unknown adjacent side length:

$$\begin{align} \tan \theta &= \frac{O}{A} \\ \end{align}$$

Re-arrange to solve for $A$:

$$\begin{align} A &= \frac{O}{\tan \theta} \\ \end{align}$$

Plug in the values and solve:

$$\begin{align} A &= \frac{O}{\tan \theta} \\ &= \frac{35\text{mm}}{\tan 63^{\circ}} \\ &= 17.8\text{mm} \\ \end{align}$$

Law of Sines

The Equation

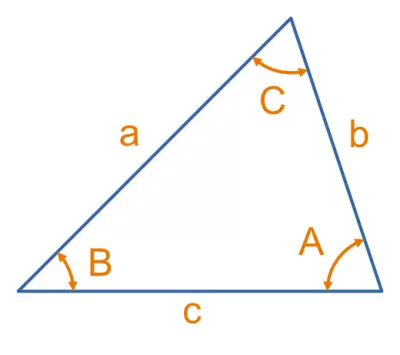
The Law of Sines is a useful equation for determining unknown lengths and angles of any triangle (not just right-angled triangles) if you know some of the other lengths and angles. Together with the Law of Cosines you can find the lengths and angles of any triangle as long as you know enough values already to fully-constrain it.

Diagram illustrating the variables used in the Law of Sines.

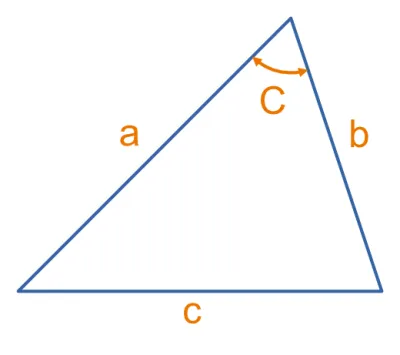
If a triangle has lengths of $a$, $b$, and $c$ and opposite angles of $A$, $B$, and $C$ respectively (as shown in the above diagram), then the Law of Sines is:

$$\begin{align} \frac{\sin{A}}{a} = \frac{\sin{B}}{b} = \frac{\sin{C}}{c} \end{align}$$

This means that the sine of the angle divided by the opposite length is the same value for all three angle/side pairs.

What Are Opposite Angles?

The opposite angle for any side of a triangle is the angle which does not “touch” the side in question. For example, if $a$ was a side of a triangle, then it’s opposite angle $A$ would be the angle enclosed by sides $b$ and $c$. The angle is directly “opposite” the side.

Tip

The lengths $a$, $b$, and $c$ and opposite angles of $A$, $B$, and $C$ may be moved around the triangle, the letters do not have a particular “side” they belong to. What is important is that $A$ is always the angle opposite side $a$ and so on.

Basic Law of Sines Calculation

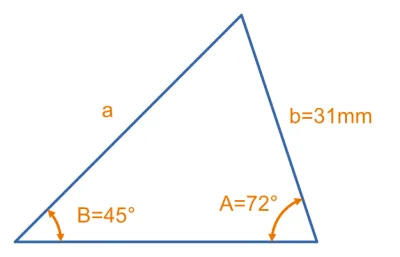
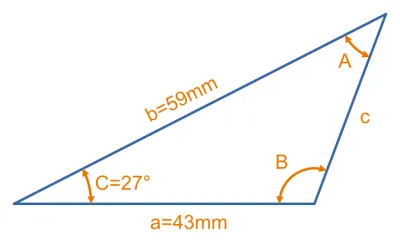
Given the triangle shown below, calculate the length of side $a$.

Diagram for Example 1.

We’ll flip the Law of Sines equation and just use one equality:

$$\begin{align} \frac{a}{\sin{A}} = \frac{b}{\sin{B}} \end{align}$$

Re-arranging for $a$:

$$\begin{align} a = \sin{A}\frac{b}{\sin{B}} \end{align}$$

Plugging in the numbers:

$$\begin{align} a &= \sin{A}\frac{b}{\sin{B}} \\ &= \sin{(72^{\circ})}\frac{31\text{mm}}{\sin{(45^{\circ})}} \\ &= 47.1\text{mm} \\ \end{align}$$

Multiple Solutions (Ambiguity)

In certain circumstances, there is more than one possible answer when calculating values using the Law of Sines. This occurs in a specific situation, when¹:

• You know the length of two sides of the triangle ($a$ and $b$) and one opposite angle $A$ (and thus are trying to calculate the other opposite angle $B$).
• Angle $A$ is in the range $0^{\circ} < A < 90^{\circ}$ (i.e. is acute).
• Length $a$ is greater than $h$ but less than $b$, where $h$ is the “vertical” height as shown below:

Diagram showing the situations when you know two sides of the triangle and 1 opposite angle. c) is the ambiguous cases which has two possible solutions.

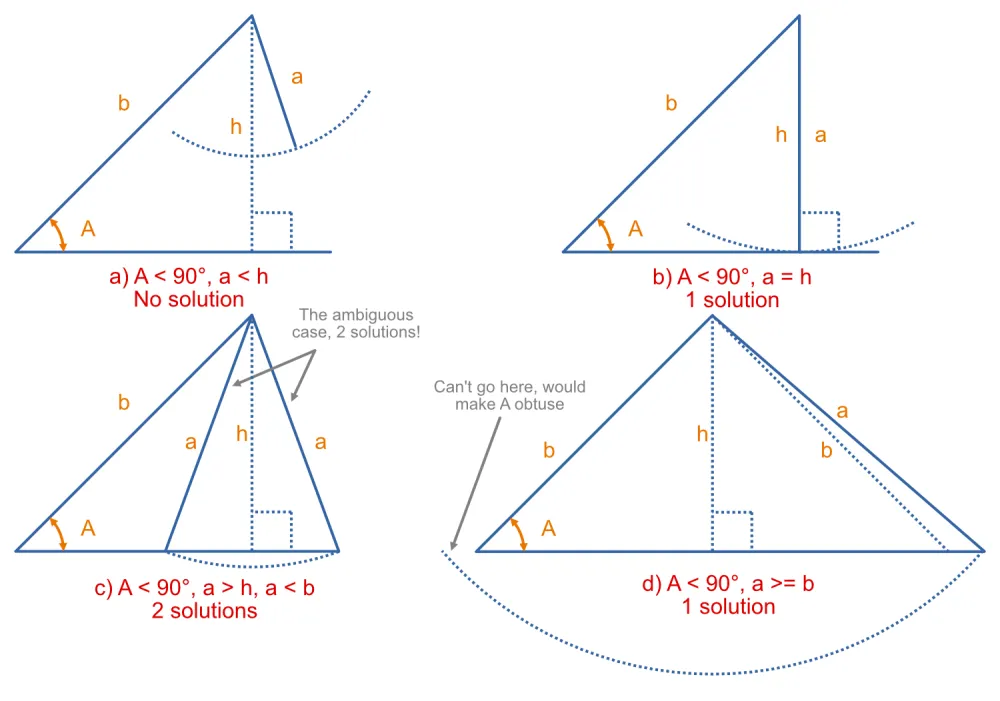
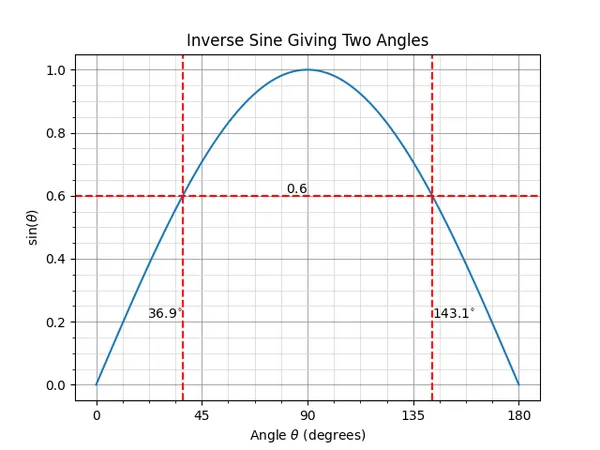
Mathematically this occurs because $\sin^{-1}$ can give two answers in the range of $[0, 180]$ (a valid angle of a triangle has to be within this range). For example, $\sin^{-1}(0.6)$ gives the following values:

$$\begin{align} \sin^{-1}(0.6) &= 36.9^{\circ} && \text{This is what the calculator will give you} \\ \sin^{-1}(0.6) &= 180.0^{\circ} - 36.9^{\circ} \\ &= 143.1^{\circ} \\ \end{align}$$

Calculators always give you the angle in the range of $[-90, 90]$ when using $\sin^{-1}$ (also called $asin$ or $arcsin$). To get the other answer you have to subtract the calculator answer from $180^{\circ}$. The image below explains the situation in visual manner.

Graph showing how inverse sine can result in two values between $[0, 180]$.

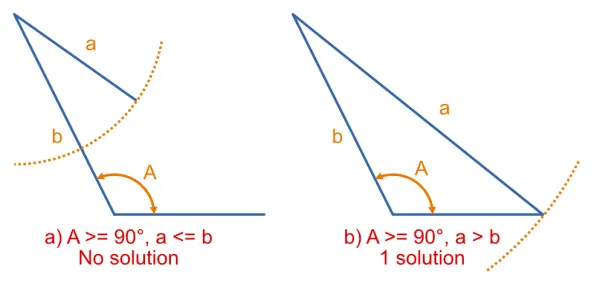
Ambiguity is not a problem if A is in the range $90^{\circ} \leq A < 180^{\circ}$ (i.e. $A$ is not acute). In this scenario, There can either be no solution or just 1 solution, but never 2. The image below illustrates this.

Diagram showing that when A is not acute, there is no ambiguous case for the Law of Sines.

If you find yourself in a position with two possible answers, what can you do? If you don’t have any other information about the triangle, then you are out of luck. However, if you know the length of the remaining side of the triangle, you can use the Cosine Law to completely solve for all angles and sides of the triangle. If you know one other angle of the triangle, then you can use the simple fact that all the internal angles sum to $180^{\circ}$ to solve for the angle you were interested in.

Ambiguous Law of Sines

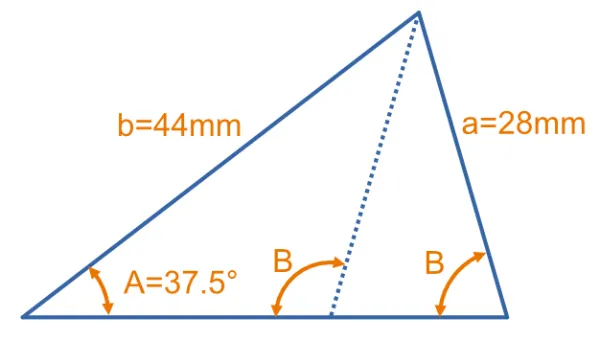
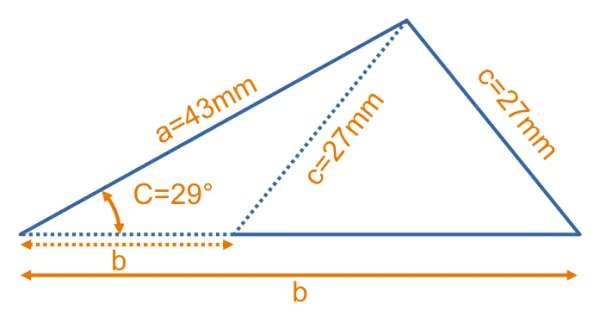
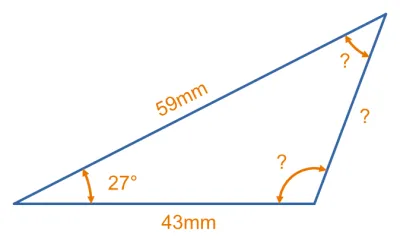
Given the triangle shown below, calculate the angle of $B$. This triangle has been designed to be ambiguous (two possible answers).

Diagram for the ambiguous Law of Sines worked example.

Let’s start with the Law of Sines equation:

$$\begin{align} \frac{\sin{A}}{a} = \frac{\sin{B}}{b} \end{align}$$

Re-arrange to solve for $B$:

$$\begin{align} B = \sin^{-1}\left(\frac{b\sin{A}}{a}\right) \end{align}$$

Plugging in the values:

$$\begin{align} B &= \sin^{-1}\left(\frac{44\text{mm} \cdot \sin{37.5^{\circ}}}{28\text{mm}}\right) \\ &= \sin^{-1}(0.957) \end{align}$$

The calculator will give us (this is the answer using the solid blue line):

$$\begin{align} B &= \sin^{-1}(0.957) \\ &= 73.1^{\circ} \end{align}$$

And the other solution is $180$ minus this (this is the answer using the dotted blue line):

$$\begin{align} B &= 180^{\circ} - \sin^{-1}(0.957) \\ &= 107^{\circ} \end{align}$$

Law of Cosines

The Law of Cosines (also known as the cosine formula or cosine rule²) is an equation similar to the Law of Sines which lets you calculate unknown sides and opposite angles of any triangle (not just right-angled triangles) if you know some of the others.

The Equation

The Law of Cosines equation is:

$$\begin{align} c^2 &= a^2 + b^2 - 2ab\cos{C} \\ \end{align}$$

where:
$a$, $b$ and $c$ are side lengths of the triangle
$C$ is the opposite angle of side $c$

The image below shows the side and angles involved in the Law of Cosines equation. Knowing all but one of these values, you can calculate the last one by re-arranging the equation.

Diagram showing the sides and angles involved in the Law of Cosines.

The law of cosines is useful for solving the sides and angles of a triangle when all three sides are known, or two sides and their included angle are known. If you know two angles and a side, or two sides and an angle other than the included angle, use the law of sines instead.

Here is the Law of Cosines equation rearranged for all sides and angles²:

$$\begin{align} a &= b\cos C \pm \sqrt{c^2 - b^2 \sin^2 C} \\ \label{law-of-cosines-solve-for-b} b &= a\cos C \pm \sqrt{c^2 - a^2 \sin^2 C} \\ c &= \sqrt{a^2 + b^2 - 2ab\cos{C}} \\ C &= \cos^{-1}\left( \frac{a^2 + b^2 - c^2}{2ab} \right) \\ \end{align}$$

Because the side and opposite angle pairs can be assigned freely around the triangle, the equation for $b$ is essentially the same as for $a$. Note that for both of these sides, there may be 0, 1 or 2 solutions.

The Law of Cosines can be thought of as a generalization of Pythagorean Theorem (the Pythagorean Theorem is the equation $c^2 = a^2 + b^2$ that applies to right-angled triangles).

If we start with the Law of Cosines equation and then make the angle $C = 90^{\circ}$ it reduces down to the Pythagorean equation:

$$\begin{align} c^2 &= a^2 + b^2 - 2ab\cos{C} \nonumber \\ c^2 &= a^2 + b^2 - 2ab\cos{90^{\circ}} \nonumber \\ c^2 &= a^2 + b^2 - 2ab\cdot 0 \nonumber \\ c^2 &= a^2 + b^2 \\ \end{align}$$

2 Sides and Their Included Angle Known

Given the triangle and known dimensions as shown below, calculate all unknown sides and angles.

Diagram for the worked example using the Law of Cosines on a triangle with 2 sides and their included angle known.

Given we know the values of two of the sides and their included angle, the Law of Cosines can help us solve for the remaining dimensions. Let’s assign letters to each of the sides and angles (we assign $C$ to the known angle, just so we can use the Law of Cosine equation verbatim without any swapping of the variable names for the first equation):

Variable names have been added.

We can now use the Law of Cosines to solve for side $c$:

$$\begin{align} c &= \sqrt{a^2 + b^2 - 2ab\cos{C}} \nonumber \\ &= \sqrt{(43\text{mm})^2 + (59\text{mm})^2 - 2\cdot 43\text{mm} \cdot 59\text{mm} \cdot \cos{27^{\circ}}} \nonumber \\ &= 28.4\text{mm} \\ \end{align}$$

Now we can use the Law of Cosines again to solve for angle $A$ or $B$. It doesn’t matter which one we pick, so lets go with $A$. We’ll pretend $A$ is the $C$ in the law of cosines diagram, as we know the length of both sides included in this angle, as well as the length of the opposite side. Swapping the variable names around happens often, just make sure to keep the opposite angles in sync also!

$$\begin{align} A &= \cos^{-1}\left( \frac{b^2 + c^2 - a^2}{2bc} \right) \nonumber \\ &= \cos^{-1}\left( \frac{(59\text{mm})^2 + (28.4\text{mm})^2 - (43\text{mm})^2}{2\cdot 59\text{mm} \cdot 28.4\text{mm}} \right) \nonumber \\ &= \cos^{-1}0.728 \nonumber \\ &= 43.3^{\circ} \\ \end{align}$$

We could use the Law of Cosines again to find the last unknown, angle $B$, but it’s far easier just to use the rule that all the internal angles of a triangle must sum to $180^{\circ}$.

$$\begin{align} B &= 180^{\circ} - A - C \nonumber \\ &= 180^{\circ} - 43.3^{\circ} - 27^{\circ} \nonumber \\ &= 110^{\circ} \\ \end{align}$$

All done!

Multiple Solutions (Ambiguity)

Just like the Law of Sines, the Law of Cosines can also have multiple solutions. And just like with the Law of Sines, multiple solutions can only occur if you know the length of two sides and one opposite angle.

Multiple Solutions with the Law of Cosines

Given the triangle below, calculate the length of side $b$.

Diagram for the worked example for the Law of Cosines that has multiple solutions.

We’ll need to re-arrange the Law of Cosines equation to solve for $b$, which has already be done for us above in $Eq.\ \ref{law-of-cosines-solve-for-b}$.

$$\begin{align} b &= a\cos C \pm \sqrt{c^2 - a^2 \sin^2 C} \\ \end{align}$$

Plugging in the values:

$$\begin{align} b &= 43\text{mm}\cos{29^{\circ}} \pm \sqrt{(27\text{mm})^2 - (43\text{mm})^2 \sin^2 {29^{\circ}}} \nonumber \\ &= 37.6\text{mm} \pm 17.2\text{mm} \nonumber \\ &= 20.4\text{mm}, 54.8\text{mm} \\ \end{align}$$

Calculators

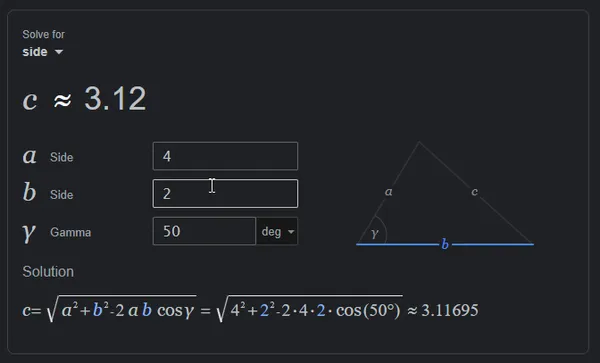
Google has handy Law of Sines/Cosines calculators that pops up when you search “law of sines”/“law of cosines”. The image below shows a screenshot of the Law of Cosines calculator.

Screenshot of the Law of Cosines calculator Google provides when you search “law of cosines”³.

The eMathHelp Law of Cosines calculator as shown below is different from most and shows you the working to solve the triangle. They also has a Law of Sines calculator.

Screenshot of the Law of Cosines calculator from eMathHelp that shows the step-by-step working to the solution⁴.

Footnotes

1. Libretexts: Mathematics. 2.1: The Law of Sines. Retrieved 2023-12-31, from https://math.libretexts.org/Bookshelves/Precalculus/Elementary_Trigonometry_(Corral)/02%3A_General_Triangles/2.01%3A_The_Law_of_Sines ↩

2. Wikipedia (2023, Dec 27). Law of cosines. Retrieved 2024-01-03, from https://en.wikipedia.org/wiki/Law_of_cosines. ↩ ↩²

3. Google. Law of Cosines [Search Results]. Retrieved 2024-01-03, from https://www.google.com/search?q=law+of+cosines. ↩

4. eMathHelp (2024). Law of Cosines Calculator - Solve triangles using the law of cosines. Retrieved 2023-01-06, from https://www.emathhelp.net/en/calculators/geometry/law-of-cosines-calculator/. ↩