The Sigmoid Function

The sigmoid function is a mathematical function which when plotted, has a characteristic “S” shape or sigmoid curve. Sigmoid curves include many cumulative distribution functions (CDFs), including the CDF of the normal distribution. They are also used in neural networks as an activation function.

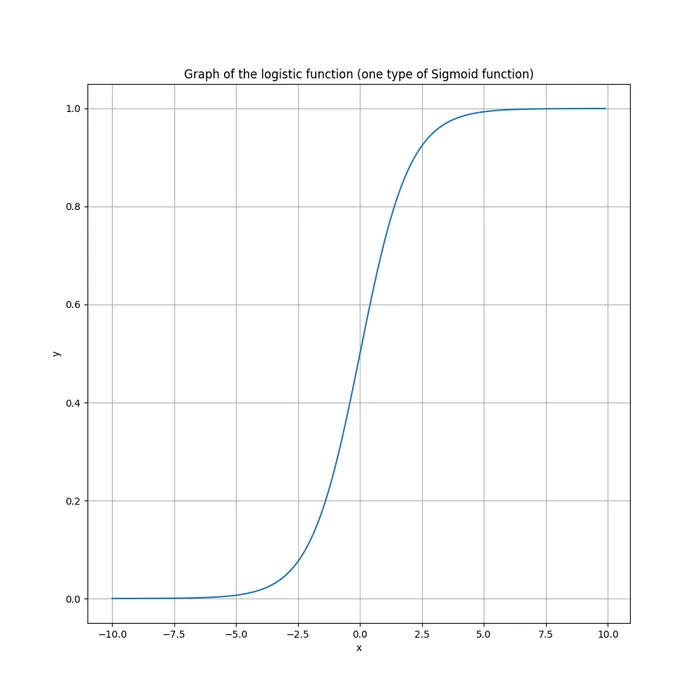
Logistic Function

The logistic function is given by the following equation:

$$ S(x) = \frac{1}{1 + e^{-x}} $$

Plotted from \(x = -10\) to \(x = 10\), the function looks like this:

The logistic function pops up in logistic regression (a popular algorithm used in machine learning) in the form:

$$ P = \frac{1}{1 + e^{-(a + b_i X_i)}} $$

where:
\(P\) is the probability of success (\a, b_i\) are coefficients \(X_i\) are feature variables