The Three Classical Pythagorean Means

Overview

In mathematics, there are many different types of “mean”. The most common type of mean is the arithmetic mean (AM), which along with the geometric mean (GM) and the harmonic mean (HM), form the three classical Pythagorean means. They are called the Pythagorean means because they were studied by Pythagoras and later generations of Greek mathematicians with their use in geometry and music¹.

Arithmetic Mean (AM)

For a set of positive, real numbers \( x = ( x_1, x_2, ..., x_n ) \), the arithmetic mean is defined by²:

$$ AM(x) = \frac{1}{n} \sum_{i=1}^{n} x_i $$

For example, the arithmetic mean of the numbers \( x = (2, 5, 6) \) is:

$$\begin{align} AM &= \frac{1}{3} (2 + 5 + 6) \\ &= \frac{1}{3} (13) \\ &= 4.33 \end{align}$$

The arithmetic mean is the most commonly used form of mean, and is typically just referred to as the “mean” of a set of numbers.

Geometric Mean (GM)

For a set of positive, real numbers \( x = ( x_1, x_2, ..., x_n ) \), the geometric mean is defined by²:

$$ GM(x) = \large{ \sqrt[n]{ \Pi_{i=1}^n x_i } } $$

where:
\( \Pi \) is the product of the terms

For example, the geometric mean of the numbers \( x = (2, 5, 6) \) is:

$$\begin{align} GM &= \sqrt[3]{(2 * 5 * 6)} \\ &= \sqrt[3]{13} \\ &= 3.91 \end{align}$$

The geometric mean is named so because it happens to be the middle number in a geometric progression. A geometric progression

The geometric means of 2 and 3 numbers can be intuitively visualized:

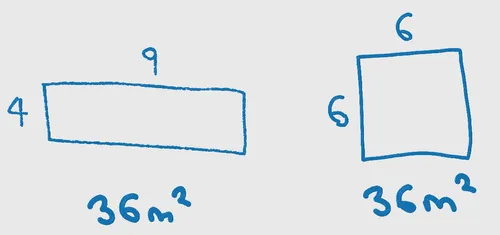
1. In 2D, it two numbers were the width and height of a rectangle, the geometric mean gives you the length of the side of a square (equal sided rectangle) which would have the same area as the rectangle.

   

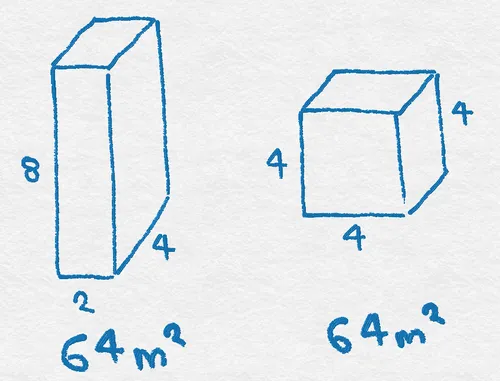
2. Similarly, in 3D if the three numbers were the width, height and depth of a rectangular cuboid (box), the geometric mean gives you the length of the side of a cube (equal sided cuboid) which would have the same volume.

   

Uses

The geometric mean is really useful when we want to compare things, where each “thing” has multiple properties which have different ranges. For example:

• Car 1 has a mileage of 25km/l and a user rating of 6/10
• Car 2 has a mileage of 20km/l and a user rating of 9/10

If we calculate the geometric mean of the mileage and rating for each car:

• Car 1: \( \sqrt{25*6}\,= 12.2 \)
• Car 2: \( \sqrt{20*9}\,= 13.4 \)

The geometric mean suggests that Car 2 may be better! The geometric mean does now skew the results like the arithmetic mean would due to the larger values for the mileage compared with the user rating. The arithmetic mean would of given \(15.5\) for Car 1 and a lower \(14.5\) for Car 2. Instead it is influenced by the proportional change of each feature, such that the larger percentage increase in the user rating for Car 2 was weighted better than the smaller percentage decrease in mileage.

The geometric mean is also useful in calculating compound interest. Let’s pretend you have $100. You made $3 of interest in the first year and $5 in the second year. If you calculated your average amount of return using the arithmetic mean, you would get $4. However, if you used the geometric mean you would get $3.87, which would be the true rate of return assuming you re-invested the $3 you made at the end of the first year (so that you had $103 earning interest for the second year).

Harmonic Mean (HM)

For a set of positive, real numbers \( x = (x_1, x_2, ..., x_n) \), the harmonic mean is defined by¹²:

$$ HM(x) = \frac{n}{ \sum_{i=0}^n x_i } $$

For example, the harmonic mean of the numbers \( 2, 5, 6 \) is:

$$\begin{align} HM &= \frac{3}{ \frac{1}{2} + \frac{1}{5} + \frac{1}{6} } \\ &= \frac{3}{0.87} \\ &= 3.46 \end{align}$$

For all positive data sets containing at least one pair of non-equal values, the harmonic mean is always the least of the three means².

The harmonic and arithmetic means are reciprocal duals of each other, when all of the values in the set are positive:

$$ HM(\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}) = \frac{1}{ GM(x_1, x_2, ..., x_n) } $$

Uses

The harmonic mean is used to calculate the \( F_1 score \) when performing classification. This is useful in classification algorithms such as logistic regression.