Bresenham's Line Algorithm

mbedded.ninja Author

Bresenham's line algorithm is way of drawing a line between two points, $A$ and $B$ on a computer screen of pixels. While this is somewhat trivial to do with floating point arithmetic, the key idea in Bresenham's line algorithm is to avoid expensive floating point arithmetic, and use integer maths only. This algorithm was invented at a time when floating-point units (FPUs) in CPUs where a lot rarer than they are today. It still has application in todays world for GPUs and other devices where FPUs are not available.

To simplify the problem, we will look at drawing a line where:

$x_1 < x_2$ and $y_1 < y_2$
The slope (gradient) of the line, $m$ is $0 < m <= 1$

Although we make these simplifications to explain the algorithm, Bresenham's line algorithm is easily extendible to draw any line (this will be shown later).

We start at the start pixel, $x_k,\;y_k$ , and we increase $x$ by 1. Then we decide on whether $y$ needs to increase by 1, or remain at $y$ . We make this decision based on whether the pixel $x_k + 1,\;y_k$ or the pixel $x_k + 1,\;y_k + 1$ is closest to the line.

Choosing the next pixel when drawing a line. Each grid point is the center of a pixel. The blue dot is the previously selected pixel that has been drawn. We have to choose the next pixel from the two possible orange options.

So in the example above, we would want to choose the pixel where we increment $y$ by 1, as you can see it is closer to the line. To work this out in code, we keep track of the amount of accumulated error between the line and the chosen pixels (error in the vertical, or y, direction only). If the error becomes larger than 0.5, we know that the $y_{k+1}$ pixel is closer to the line than the $y_k$ pixel, and we increment $y$ by 1.

The below python code shows this by example:

def draw_line_tracking_error(x_start, y_start, x_end, y_end):
    slope = (y_end - y_start)/(x_end - x_start) 
    error = 0
    curr_y = y_start
    for x in range(x_start, x_end + 1):       
        draw_pixel(x, curr_y)
        # Now we just keep track of the error,
        # and if it is > 0.5, increment y
        # We are still using floating-point arithmetic though!
        error += slope
        if error > 0.5:
            curr_y += 1
            error -= 1 # error drops by 1 since we increment y

Note we are still using float-point arithmetic. There are further optimizations we can do to remove floats altogether.

Remember that the error ( $\epsilon$ ) + the slope ( $\frac{\Delta y}{\Delta x}$ ) must be less than 0.5 for y to not be incremented:

\epsilon + \frac{\Delta y}{\Delta x} < 0.5

Consider the above equation the "check" we will do to see if we increment y (the if statement). We want to get rid of all possible non-integer values from this equation. The two non-integer values are the slope, and the 0.5. Let's manipulate this equation to remove them.

First, we multiply everything by $\Delta x$ to get rid of the fraction:

\epsilon \Delta x + \Delta y < 0.5 \Delta x

We can then multiply everything by 2 to get rid of last float, the 0.5:

2 \epsilon \Delta x + 2 \Delta y < \Delta x

Tada! The above equation only contains integers. We can implement this check in code as shown below:

def draw_line_bresenham(x_start, y_start, x_end, y_end):
    """
    Implementation of Bresenham's line algorithm in Python. This will work for positive sloped lines
    with a gradient between 0 and 1 only. Also, x_start < x_end and y_start < y_end must be true.
    """
    dy = y_end - y_start
    dx = x_end - x_start

    # Note that the initial error does not start at zero!
    error = 2*dy - dx    
    y = y_start
    for x in range(x_start, x_end + 1):       
        print(f'x = {x}, y = {y}')
        
        # If error integer is > 0, we need to increment y and
        # update error
        if error >= 0:
            y += 1
            error -= 2*dx            
        
        error += 2*dy

If the programming language supports it, you can perform the *2 multiplication above with a left-shift (a good compiler will probably optimize this for you anyway).

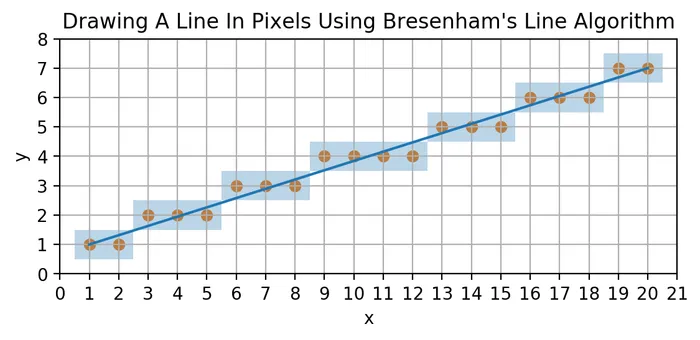
A line drawn using Bresenham's line algorithm.

It also helps to see Bresenham's line algorithm in action on a larger line:

For comparison, if we don't care about using floating point arithmetic (and we don't want to use Brehenham's line algorithm), we can just use the simple method below:

def draw_line_simple(x_start, y_start, x_end, y_end):
    slope = (y_end - y_start)/(x_end - x_start)    
    
    for x in range(x_start, x_end + 1):        
        # Works but is "slow", floating point addition/multiplication on every pixel increment
        y_true = slope*(x - x_start) + x_start
        y_pixel = round(y_true)
        draw_pixel(x, y_pixel)