RC Charging Circuits

RC charging circuits are circuits which charge a capacitor through a resistor. They appear in almost all electronic designs in some form or another. They are used for things such as simple time delays, primitive oscillators, debouncing, and filtering.

This page looks at how the RC circuit responds in the time domain. If you are interested in it’s frequency response, see the Analogue Filters page.

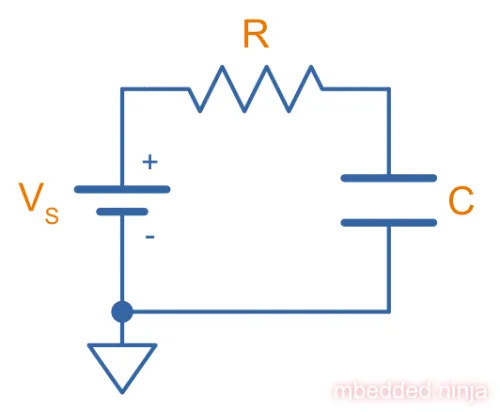
The Circuit

A basic RC charging circuit.

Assuming the capacitor’s voltage started at $0V$ at $t=0$, and a constant supply voltage $V_S$ is applied across the capacitor and resistor, then the capacitors voltage at any time $t$ is¹:

$$\begin{align}\Large{ V_C = V_S (1 - e^{ \left[ \frac{-t}{RC} \right] }) }\end{align}$$

where:
$V_C$ is the voltage across the capacitor, in Volts
$V_S$ is the supply voltage, in Volts
$e$ is Euler’s number, $= 2.718...$
$t$ is the time, in seconds
$R$ is the resistance, in Ohms
$C$ is the capacitance, in Farads

$RC$ can be replaced with a concept called a time constant, where $\tau \equiv RC$. This gives:

$$\begin{align} \Large{ V_C = V_S (1 - e^{ \left[ \frac{-t}{\tau} \right] }) } \end{align}$$

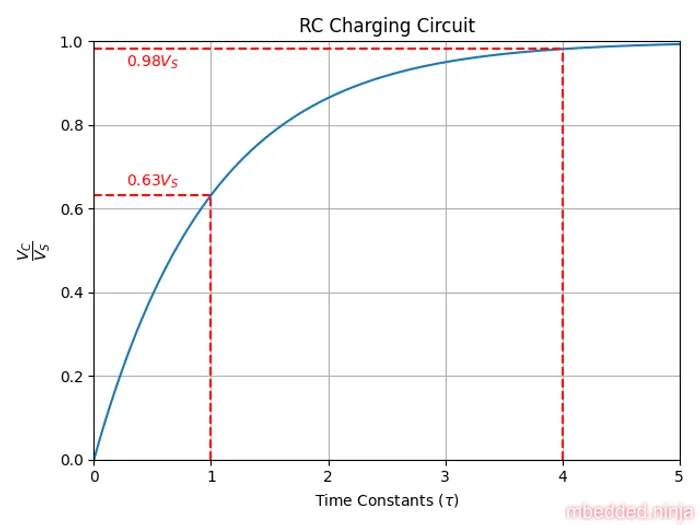
The capacitor voltage with respect to time is shown below.

A basic RC charging circuit.

Tip

The Y-axis is just which the equation re-arranged to:

$$\begin{align} \frac{V_C}{V_S} = 1 - e^{ \left[ \dfrac{-t}{RC} \right] } \end{align}$$

The capacitors voltage $V_C$ starts of a $0V$ and charges towards $V_S$. However the charging rate follows an exponential decay, the rate gets slower and slower. Mathematically, the capacitors voltage never reaches $V_S$. However for most practical purposes you can consider the capacitor “fully-charged” after about 5 time constants.

What is the Time Constant?

The time constant is a way of simplifying the analysis of an RC circuit and lets you think and talk about the circuit in a consistent manner.

$$\begin{align} \tau \equiv RC \end{align}$$

After 1 time constant ($t = 1\tau$), then the equation simplifies to:

$$\begin{align} \frac{V_C}{V_S} &= 1 - e^{ \left[ \dfrac{-t}{RC} \right] } \\ &= 1 - e^{ \left[ \dfrac{-1\tau}{\tau} \right] } \\ &= 1 - e^{ \left[ -1 \right] } \\ &= 1 - 0.368 \\ &= 0.632 \end{align}$$

So you know that at $1\tau$, your capacitor has charged to 63% of the supply voltage. The beauty of $\tau$ is that you can quickly calculate it for any RC circuit and get a feel for how long it will take to charge (it is also very useful when looking at RC filters). The table below shows various time constants and the voltage level on the capacitor at that point.

Time Constant	Voltage as Percentage of Supply
1$\tau$	63.2%
2$\tau$	86.5%
3$\tau$	95.0%
4$\tau$	98.2%
5$\tau$	99.3%

Tip

The percentages in the above table were calculated with:

$$\begin{align} \text{perc} = (1 - e^{-\tau}) \times 100 \end{align}$$

Note that by 5 time constants, the voltage is at 99.3% of the supply voltage. This is generally considered to be the point at which it is “fully charged”.

Footnotes

1. Electronics Tutorials. RC Charging Circuit. Retrieved 2024-02-16, from https://www.electronics-tutorials.ws/rc/rc_1.html. ↩