Convex Hull Algorithms

Overview

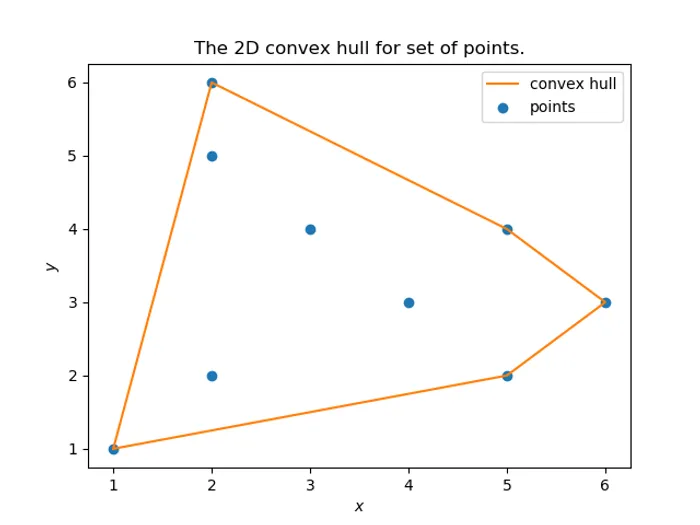
Given a cloud of points on a 2D plane, a convex hull is the smallest set of points which encloses all of the points.

Another useful concept related to convex hulls is the minimum bounded rectangle. The minimum bounded rectangle is the smallest rectangle (measured by area) which encompasses the entire convex hull (by extension, it is also the smallest rectangle that encompasses all points).

The minimum bounded rectangle must have an edge which is co-linear to one of the edges in the convex hull.

The Jarvis March (Gift Wrapping Algorithm)

Orientation:

• If \(o == 0\) they are co-linear
• If \(o > 0\) they are clockwise
• If \(o < 0\) they are counter-clockwise

This equation comes from the 3D definition of the cross-product (for a proof, see here).

1. Pick one point that is guaranteed to lie in the convex hull. This can be done by picking the left-most point (i.e. has the lowest x value). If there is more than one point that meets this condition, you are free to choose any one. Add this to the start of list of the convex_hull points.
2. Pick any other point to be the potential next_point on the hull.
3. Iterate over all the points, checking the orientation between the last_point found on the hull, the potential next_point, and the loop_point you are currently iterating over. If the orientation is counter-clockwise, then loop_point is to the left the the line formed by between last_point and next_point, and becomes the next_point.
4. One you reach the end of the loop, next_point is guaranteed to be the correct next point on the convex hull. Append this to the convex_hull list.
5. Repeat steps 2 to 4, until you end up adding the same point to the convex_hull list as you started with (the left most point).
6. Done!

Scipy

scipy provides a ConvexHull object which can be used to calculate a convex hull from a set of points.

Shapely

The Shapely library for Python has built-in support for finding the minimum bounded rectangle for a generic geometry type. Shapely can find the minimum bouded rectangle for polygons, point sequences, e.t.c.

1

BaseGeometry.minimum_rotated_rectangle()

1
2
3
4
5
6
7
8

Polygon([
  [1, 1],
  [2, 1],
  [5, 4],
  [4, 3],
  [6, 2],
])

Other Resources

https://www.geometrictools.com/Source/ComputationalGeometry.html contains some useful geometric algorithms for C/C++, including convex hull algorithms and code for finding the minimum bounding box/volume/circle/sphere e.t.c.

https://stackoverflow.com/questions/13542855/python-help-to-implement-an-algorithm-to-find-the-minimum-area-rectangle-for-gi contains useful information to fin the minimum bounded rectangle.

https://www.geometrictools.com/Documentation/MinimumAreaRectangle.pdf is a very detailed and precies explanation on how the minimum bounded rectangle algorithm works. See here for a cached copy.