Gates

Logic gate inputs are normally labelled as a single letter, starting with A (e.g. a three input AND gate would have inputs A, B and C). The output is normally labelled Y (in other material you may see this labelled X), unless you are using a flip-flop or latch, and the output is labelled Q.

There are a few different standards used to draw logic gates on schematics:

• MIL-STD-806B (Graphic Symbols For Logic Diagrams): This most commonly used symbols for basic and/or/xor e.t.c gates is captured in this standard. Each gate has a unique shape and are easily distinguished on a large schematic with many gates. NOT logic is shown with a bubble.
• IEC 60617 (ANSI/IEEE Std 91-1984): All the gates are IC-like rectangles with symbols inside to denote the function. NOT logic is shown with a flag on the pin rather than a bubble. Not as easy too quickly identify the gate as MIL-STD-806B, and not as widely used.
• DIN 40700-24 (Graphical Symbols; Components For Precision Engineering Devices, Especially Clocks): Ever rarer than the MIL-STD-806B or IEC 60617 symbols, these are rarely seen. The 1976 Edition was released in June 1976. DIN symbols on this page are referenced to https://de.wikipedia.org/wiki/Logikgatter#Typen_von_Logikgattern_und_Symbolik.

This page uses the convention of TRUE or 1 to represent the logic state true, and FALSE or 0 to represent the logic state false.

Types of Gates

NOT

Arguably the simplest logical gate (ignoring a buffer), a NOT gate (a.k.a. inverter) always outputs the opposite (complement) of the input. If the input is TRUE, the output is FALSE. If the input is FALSE, the output is TRUE.

The symbols for a NOT gate (inverter).

Tip

Although almost never shown on basic diagrams (but always shown somewhere on proper circuit schematics), aside from the inputs and outputs, all gates also need power pins to provide power for the internal logic.

The truth table for an NOT gate is:

Inputs	Output
A	Y
0	1
1	0

And this gives rise to the simple equation for NOT logic:

$$\begin{align} Y = \overline{A} \end{align}$$

AND

An AND gate outputs TRUE only if all it’s inputs are TRUE. AND is also called logical conjunction¹.

The symbols for an AND gate.

Truth table for an AND gate is:

Inputs		Output
A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

The equation for the AND logic may be written in one of the following ways:

$$\begin{align} Y &= A \cdot B \ \text{(preferred)} \\ Y &= AB \\ Y &= A \& B \\ Y &= A \wedge B \\ \end{align}$$

An AND gate can be made using basic diode logic as shown below:

An AND gate made from basic diode logic.

NAND

A NAND gate is just an AND gate but with the output inverted. This is shown below with the bubble at the output of the AND symbol:

The symbol for an NAND gate.

Truth table for an NAND gate:

Inputs		Output
A	B	Y
0	0	1
0	1	1
1	0	1
1	1	0

OR

A OR gate is TRUE if at least one input is TRUE. This means it is also outputs TRUE if all it’s inputs are TRUE. OR is also called logical disjunction¹.

The symbol for an OR gate.

Truth table for an OR gate:

Inputs		Output
A	B	Y
0	0	0
0	1	1
1	0	1
1	1	1

The OR operation can be expressed in an equation in the following ways:

$$\begin{align} Y &= A + B \ \text{(preferred)} \\ Y &= A \vee B \\ Y &= A || B \\ \end{align}$$

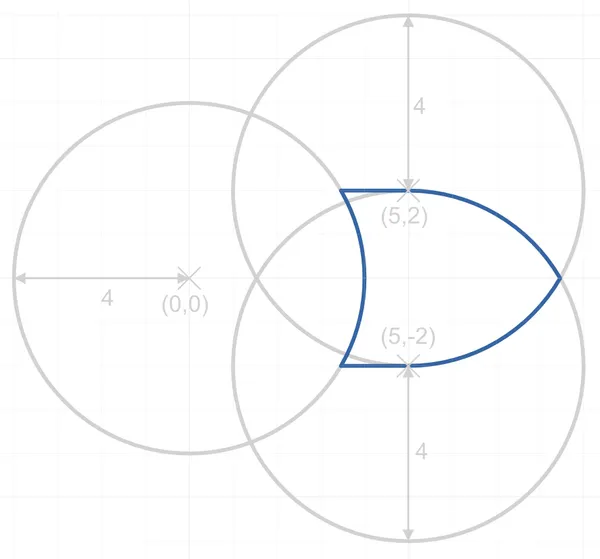
The OR gate be drawn using three equal diameter circles placed on a grid as shown in the below image. Segments of the circles perimeters are taken along with the addition of two horizontal line sections to form the classic OR gate shape².

Diagram showing how to draw an OR gate from the segments of three equal diameter circles placed on a grid².

NOR

A NOR gate is just a OR gate but with the output inverted (i.e. what you would get if you connected the output of an OR gate to an inverter). Just like the NAND gate, the NOR is gate is shown in the below image — and is just an OR gate symbol with a bubble on the output.

The symbols for a NOR gate.

Truth table for an NOR gate:

Inputs		Output
A	B	Y
0	0	1
0	1	0
1	0	0
1	1	0

The equation for an NOR gate:

$$\begin{align} Y = \overline{A + B} \end{align}$$

XOR

A 2-input XOR gate (exclusive OR) only outputs TRUE if one and only one of it’s inputs is also TRUE. For many gate construction technologies, the XOR gate is the most complex primitive gate to build.

The symbols for a 2-input XOR (exclusive-or) gate.

Truth table for a 2-input XOR gate:

Inputs		Output
A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

Note

The only difference in behaviour between an OR and XOR is when both inputs are TRUE. An OR gate outputs a TRUE in this case, whilst and XOR outputs a FALSE.

The symbol $\bigoplus$ is used to represent XOR, as hence XOR can be written in the following ways:

$$\begin{align} Y &= (A \cdot \bar{B}) + (\bar{A} \cdot B) \\ Y &= (A + B) \cdot (\bar{A} + \bar{B}) \\ Y &= A \bigoplus B \\ \end{align}$$

There are many ways to build XOR gates from the more basic NAND, NOR, AND and OR gates. The most intuitive approach to me is to represent the XOR gate as $Y = (A \cdot \overline{B}) + (\overline{A} \cdot B)$. The following circuit shows this structure:

A XOR gate made from AND and OR gates, with some of the inputs inverted into the front-end of the AND gates.

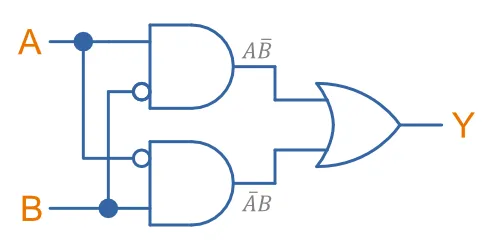
The following circuit shows a XOR gate made from a AND, NAND and OR gate. This circuit implements the equation $Y = (\overline{AB}) \cdot (A + B)$. Toggle the inputs in the right-hand side interactive simulation to see the XOR gate in action!

A XOR gate made from 1 AND, NAND and OR gate.

(full page version)

The below image shows a XOR gate made exclusively from NAND gates:

A XOR gate made exclusively from NAND gates.

You can also make a XOR gate exclusively from NOR gates, as shown in the below image. Note that the structure is similar to the all-NAND gate version of the XOR, but with the additional inverting gate on the output.

A XOR gate made exclusively from NOR gates.

Whilst it is intuitive how a AND or OR gate should work with more than 2 inputs, that same cannot be said for a XOR gate. Should the output be TRUE only if exactly one input is TRUE? Should the output be TRUE if at least 1 but not all of the inputs are TRUE? Or should the output be TRUE if one input is TRUE, FALSE for 2 inputs TRUE, TRUE again for 3 inputs TRUE, e.t.c? So in general, a XOR gate with more than 2 inputs is ill-defined. However, there are a few other names used for logic that performs some of these functions:

1. Output TRUE only if 1 and only 1 input is TRUE. This is called a one-hot detector. However, this is rarely seen in practise.
2. Output TRUE only if an odd number of inputs are TRUE. This is called a parity generator or modulo-2 adder.

XOR gates are used for:

• Parity generators: A sequence of XOR gates can calculate the parity of block of data, which is used for simple single-bit error detection in some communication protocols (e.g. optional setting you can enable with UART)³.
• Correlation/sequence detection: XOR gates output FALSE if both inputs are the same. This behaviour can be utilized to perform correlation between two bit streams.
• Cryptographic circuits.

XNOR

The XNOR gate is an XOR gate but with the output inverted. The symbol is:

The symbols for a XNOR gate.

The truth table for an XNOR gate is:

Inputs		Output
A	B	Y
0	0	1
0	1	0
1	0	0
1	1	1

Logic Families

Diode Logic (DL)

Diode logic (DL) is digital logic circuitry made from just diodes and resistors. It is a very simple (if not the simplest) way of constructing logic gates in a circuit. Diode logic is great for getting a basic theoretical understanding of how logic gates are realized, but is rarely used in practise due to fan-out, switching speed issues, and limited gate constructibility (more on this below)!. Also known as diode-resistor logic (DRL).

//

An AND gate made from basic diode logic.

Before long you’ll be struck with the solemn realization you can’t create a NOT gate (inverter) from pure diode logic (or any gates that require inverting capabilities, such as NAND or NOR gates). This limits you to being only able to make AND or OR gates, and hence it’s usefulness is severely limited. NOT gates are constructable as soon as you add switching elements, such as transistors. Resistor-transistor logic is the extension of diode logic but the addition of transistors.

Resistor-Transistor Logic (RTL)

Resistor-transistor logic (RTL) is one of the most basic families of digital logic (only diode logic beats it in terms of simplicity). It uses resistors and BJTs to build the basic gates required for digital logic. Now days it is completely superseded by logic families such transistor-transistor logic (TTL) and CMOS. However, it serves as a great place to introduces readers on how logic gates are built from discrete components.

A very basic logic “inverter” made from RTL.

Advantages:

• Very basic to create.
• Used a minimal amount of transistors (this was important in the early days of IC fabrication as transistors were expensive!)

Disadvantages:

• Very limited fan-out.
• Significant power consumption: When the transistors are switched on.
• Weak drive in one direction: Single transistor strongly drives output only in one direction, pull-up/down resistor is used in opposite direction.
• Poor noise margins.

Schematic of a RTL NOR gate. When both inputs are LOW, neither transistor is on and the output is pulled HIGH by $R_C$. Any HIGH input will turn on a transistor, which will drive the output LOW.

The Apollo Guidance Computer (AGC) used RTL logic. The AGC controlled and navigated the Apollo spacecraft to the Moon and back⁴.

Diode-Transistor Logic (DTL)

TODO: Add info here.

Transistor-Transistor Logic (TTL)

The inputs of TTL logic are the emitters of BJTs.

TTL NAND Gate

TTL NAND gates can use special multiple-emitter BJTs to reduce the transistor count. Each input of the NAND gate is connected to one of the emitters. In the case of a NPN BJT, is any 1 or more of the base-emitter junctions is forward biased, then the transistor turns on⁵.

N-type Metal-oxide Semiconductor Logic (NMOS)

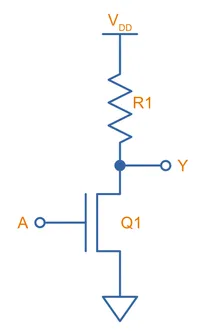
N-type Metal-oxide Semiconductor (NMOS) logic is a way of building logic functions from N-channel MOSFETs. In the early days of digital logic (1970s), it was much faster and easier to manufacture than CMOS, however since the 1980s CMOS took over and has become the dominant way of implementing logic gates⁶. NMOS is built from an arrangement of N-channel MOSFETs on the low-side (depending on the function) and a pull-up resistor on the high side.

NMOS Inverter Gate

A NMOS inverter is simply made from a N-channel MOSFET and a resistor, as shown below:

The simple inverter made using NMOS technology.

(full page version)

When the input $A$ is LOW, the N-channel MOSFET is turned OFF, and so the output $Y$ is pulled HIGH by $R1$. When $A$ is HIGH, the N-channel MOSFET gets turned on. It’s equivalent drain-source resistance drops to a value much lower than $R1$, and so therefore the output is effectively driven LOW, completing the inverter functionality.

Tip

You can see the static current flow (and therefore power consumption) in the above NMOS circuit simulation when you toggle the input to HIGH.

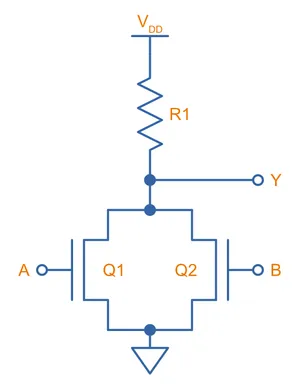
NMOS NOR Gate

The NMOS NOR gate uses two N-channel MOSFETs connected in parallel to drive the output LOW if either input is HIGH. If neither input is LOW, then no MOSFET will be on and the output will be pulled HIGH by the resistor.

A NOR gate made using NMOS technology.

(full page version)

Complementary Metal-oxide Semiconductor Logic (CMOS)

Complementary metal-oxide-semiconductor (CMOS) is a way of building logic functions from complementary pairs of N-channel and P-channel MOSFETs. Today, it is by far the most popular way of constructing digital integrated circuits (ICs)⁷. CMOS circuits typically have negligible static power dissipation and only consume power during transitions. It advances from NMOS technology by replacing the upper resistor with P-channel MOSFETs, which both eliminates static power dissipation and speeds up the low-to-high transition.

Represented by AC/ACT in part numbers, or HC/HCT for high-speed equivalents. The T in the logic subfamily name signifies the parts have TTL-compatible inputs.

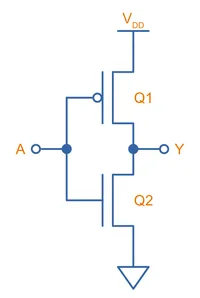
CMOS Inverter Gate

The inverter is the easiest CMOS logic gate to make! It just consists of one P-channel and one N-channel MOSFET in a “totem-pole” configuration, as shown below. On the right-hand side is an interactive simulation.

A CMOS inverter gate.

(full page version)

Tip

These diagrams use the simplified MOSFET symbols in where the P-channel as a bubble next to it’s gate and the N-channel doesn’t. No indication of drain or source are shown either, although this may be a moot point if in an integrated circuit with the substrate not connected to the source. If you are unfamiliar with this MOSFET symbol style, see the MOSFETs page for more info.

When the input $A$ is HIGH, the gate-source voltage of the bottom-side N-channel MOSFET is $+V_{DD}$ and turns the MOSFET ON. The top-side P-channel MOSFETs gate-source voltage is $0V$ and therefore OFF. Hence the output gets driven LOW. When $A$ is LOW, the bottom-side N-channel MOSFETs gate-source voltage goes to $0V$ and the P-channel’s gate-source voltage goes to $-V_{DD}$, turning it ON and driving the output HIGH.

Video of a basic CMOS inverter made from a discrete P-channel and N-channel MOSFET. The inverter is fed a 0.5Hz clock signal into it’s input from a function generator. 1 LED is connected to the inverters input, the other connected to it’s output.

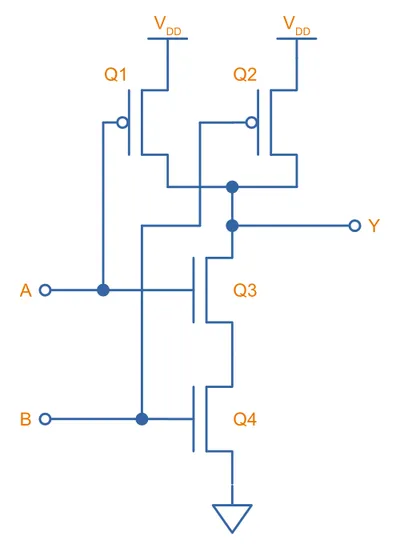
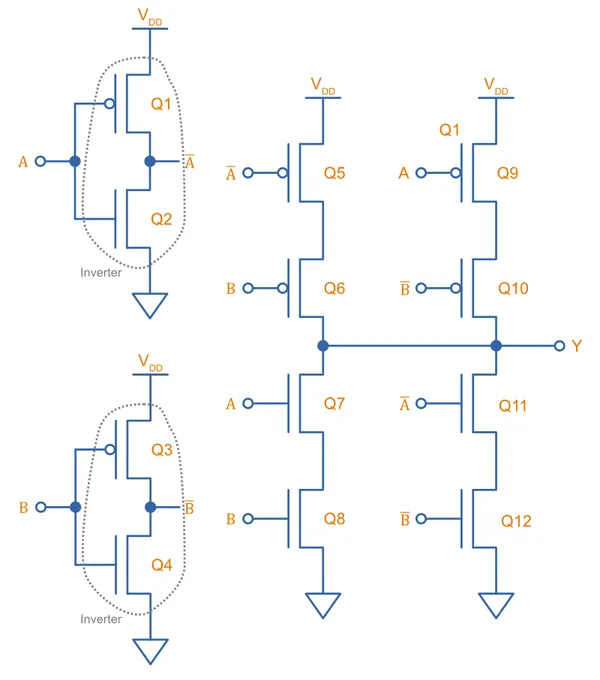
CMOS NAND Gate

After the inverter, the two easiest CMOS gates to build are the NAND and NOR gates. A 2-input NAND gate can be built from two P-channel and two N-channel MOSFETs as shown below. On the right-hand is an interactive simulation.

A 2-input CMOS NAND gate, built from two P-channel and two N-channel MOSFETs.

(full page version)

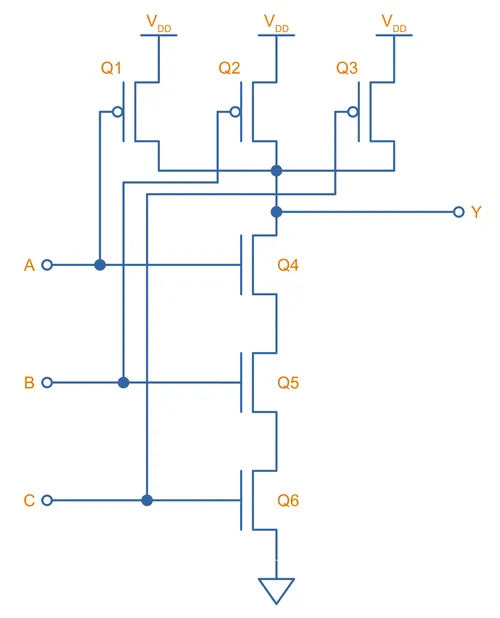
Two N-channels are connected in series on the bottom side, and two P-channels are connected in parallel on the top side. Both inputs ($A$ and $B$) have to be HIGH to turn on both the lower side N-channel MOSFETs and drive the output ($Y$) LOW. If either inputs are LOW, at least one of the high-side P-channel MOSFETs will be turned on, driving the output HIGH. This completes the NAND logic.

The number of inputs can be easily increased from 2 by adding the appropriate number of extra MOSFETs in series and in parallel. For example, a 3-input CMOS NAND gate’s schematic would look like this:

A schematic for a 3-input CMOS NAND gate.

CMOS NOR Gate

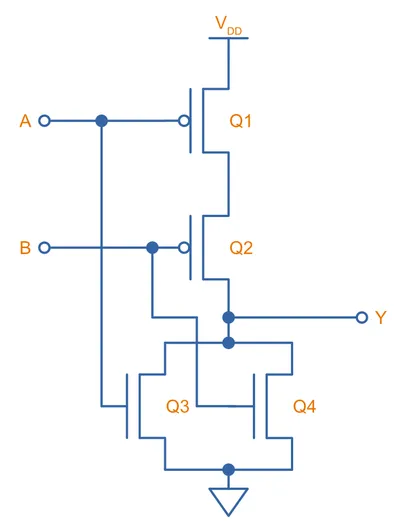
A CMOS NOR gate is built in a similar fashion to a NAND gate, except you swap the serial and parallel connections of the P-channel and N-channel MOSFETs around. On the right-hand side is an interactive simulation.

A CMOS NOR gate.

(full page version)

CMOS AND Gate

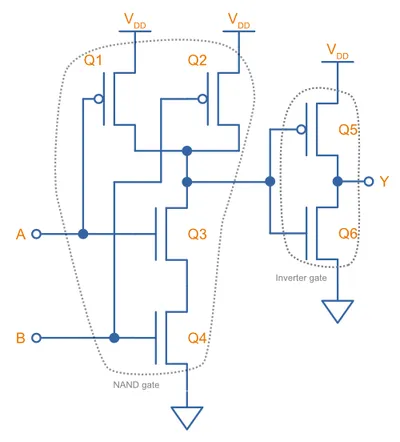
Funnily enough, the easiest way to build a CMOS AND gate to to build a NAND gate and then add an inverter on it’s output. Thus it’s schematic looks like what is shown in the below-left picture.

The schematic for building a 2-input CMOS AND gate. Notice how it’s just a NAND gate with an inverter attached to the output.

(full page version)

CMOS OR Gate

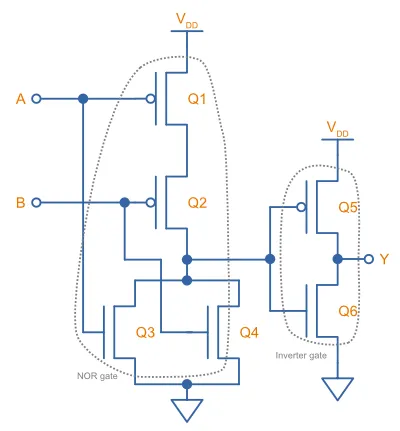
In a similar fashion to the CMOS AND gate, the simplist way to build a CMOS OR gate is to build a NOR gate and then add an inverter on it’s output.

The schematic for building a 2-input CMOS OR gate. Notice how it’s just a NOR gate with an inverter attached to the output.

(full page version)

CMOS XOR Gate

The CMOS XOR gate is the hardest CMOS gate primitive to build! It can be built with the circuit shown below, which uses a total of 12 MOSFETs, 3 times as many as the basic NAND and NOR gates!⁸

A XOR gate built from CMOS logic.

Have a play around with the interactive XOR gate simulation below:

(full page version)

Tristate CMOS Inverter

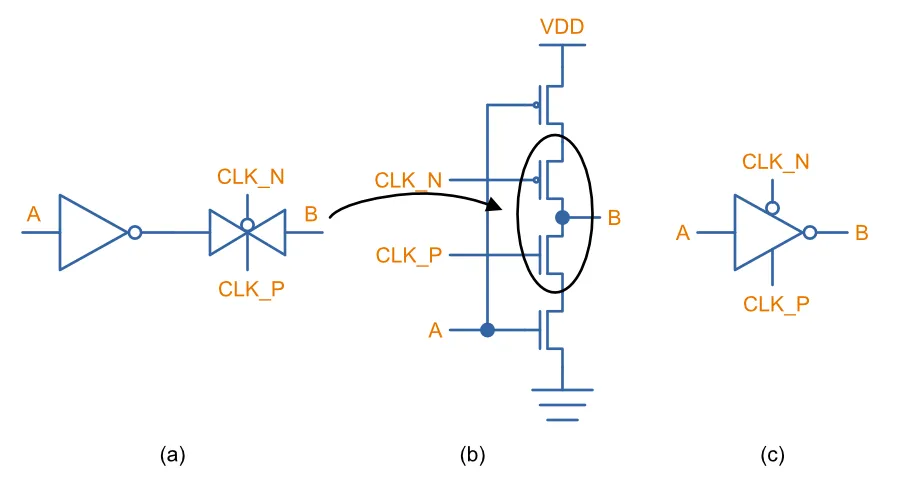
A useful building block for digital logic is a CMOS inverter whose output can also be tri-stated. The obvious way to do this would be connect the output of a regular inverter to a transmission gate, as shown in (a) in the figure below. But these MOSFETs can be recombined to make a single “totem-pole” stack which provides the same functionality, as shown in (b)⁹. In (b), the N-channel MOSFET of the transmission gate it connected in series with the N-channel MOSFET of the inverter on the lower leg. Likewise for the P-channel MOSFETs. This circuit is sometimes simplified to the symbol shown in (c).

Diagram showing how a tri-state converter can be made by combining the MOSFETs from a inverter and transmission gate into a single “totem pole” arrangement.

Pass Transistor Logic (PTL)

Pass transistor logic (PTL) is a form of logic design in where transistors are used to connect the input directly to the output — to reduce the number of transistor required to implement the logic. CMOS logic always uses the input to switch the output to either the positive rail or ground. PTL on the other hand eliminates some of the transistors that would be required in CMOS logic by allowing the transistors to connect the input directly to the output (instead of connecting the output to the rails). The disadvantage of doing this is that the output voltage reduces through each stage¹⁰.

Transmission gates are used frequently in the design of PTL logic as a way of switching the input to the output.

PTL AND Gate

An AND gate can be made from PTL logic using a total of 5 transistors, one less than the 6 required in CMOS logic.

An AND gate made from PTL logic.

The circuit on the left is just an inverter to provide $\overline{B}$ which is needed for the PTL logic on the right. The TG on the right connects $A$ to the output only if $B = 1$. Thus:

• $B = 1$ and $A = 0$, then $Y = 0$
• $B = 1$ and $A = 1$, then $Y = 1$

If $B = 0$, then the TG is off but the bottom-right N-channel MOSFET is turned on, connecting the output to $GND$ (we don’t care what $A$ is). Thus:

• $B = 0$ and $A = 0$, then $Y = 0$
• $B = 0$ and $A = 1$, then $Y = 0$

It should now be pretty clear that this works as an AND gate. Play around with the interactive simulation below:

(full page version)

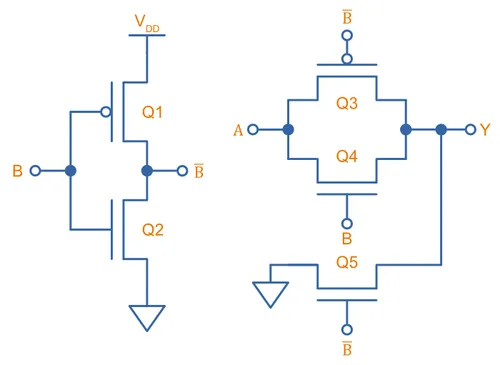
8 Transistor PTL XOR Gate

Above we showed how complex a XOR gate is to build in CMOS logic (12 transistors!). PTL logic can significantly reduce the transistor count for a XOR gate. One such implementaton is¹¹:

A XOR gate made from PTL logic. This XOR circuit uses a total of 8 transistors, less than the CMOS implementation that uses 12. But we can still do better!

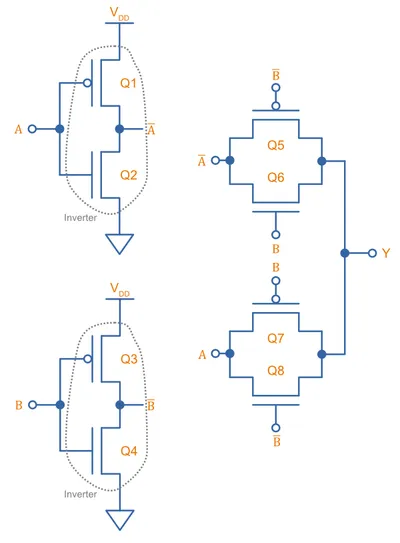
To see how this works, ignore the simple CMOS inverters on the left and focus on the PTL logic on the right. Input $B$ controls which transmission gate is on and which is off. If $B$ is LOW, the bottom transmission gate is on and the top is off, passing $A$ to the output. Thus:

• If $B = 0$ and $A = 0$, then $Y=0$
• If $B = 0$ and $A = 1$, then $Y=1$

If $B$ is HIGH the opposite happens, the top tranmission gate is on and the bottom is off, passing $\overline{A}$ to the output. Thus:

• If $B = 1$ and $A = 0$, then $Y=1$
• If $B = 1$ and $A = 1$, then $Y=0$

Now it should be pretty easy now to see that this gives you a XOR gate!

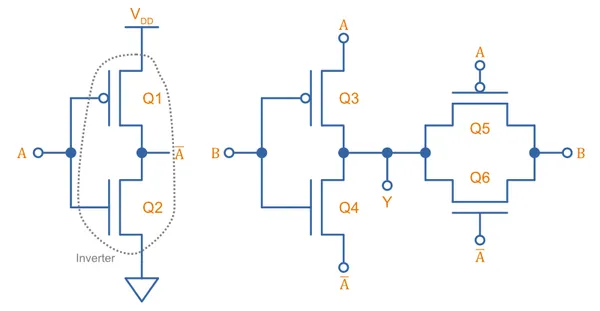
6 Transistor PTL XOR Gate

However, we can reduce the transistor count even further! This following clever circuit implements a XOR gate in PTL logic using a total of only 6 transistors¹².

A XOR gate made in PTL logic with only 6 transistors¹².

The left-side of the circuit is an “inverter” (but with the MOSFET source leads connected to $A$ rather than the rails), and the right-hand side is a transmission gate.

• When $A = 0$, both MOSFETs in the inverter will always be OFF because the gate-source voltage of the N-channel MOSFET can never be more positive than 0V and the gate-source voltage of the P-channel can never be more negative than 0V. The right-hand side transmission gate will be ON, and so the output will equal $B$.
• When $A = 1$, the transmission gate will be OFF, and the inverter will become active, passing through the inverse of $B$ to the output.

This makes a XOR gate! Have a play around with the interactive simulation of it below:

(full page version)

Logic Gate Part Numbers

Texas Instruments introduced the SN74xx series of logic ICs in the 1960s, using TTL logic. These parts became very popular and many other manufactures began making pin-compatible parts. They kept the 74xx section of the part number to aid identification, and hence the 74xx is somewhat standardized across the industry.

The 5400 series is the military rated version of the 7400 series. The 4000 series is the newer CMOS alternative to the 7400 TTL logic. However (and which is somewhat confusing), newer 7400 parts can also be made using CMOS logic, for example, the 74HC4051 analogue multiplexer¹³. These parts commonly using the logic subfamily names HC or HCT.

Part number descriptions for the popular TTL 74xx family of ICs:

Part Number	Description	Num. Units	Input	Output
74x00	Quad 2-input NAND gate	4	Normal	Push-pull
74x01	Quad 2-input NAND gate	4	Normal	Open-collector
74x02	Quad 2-input NOR gate	4	Normal	Push-pull
74x03	Quad 2-input NAND gate	4	Normal	Open-collector
74x04	Hex inverter gate	6	Normal	Push-pull
74x05	Hex inverter gate	6	Normal	Open-collector
74x06	Hex inverter gate	6	Normal	Open-collector, 30V/40mA
74x07	Hex buffer gate	6	Normal	Open-collector, 30V/40mA
74x08	Quad 2-input AND gate	4	Normal	Push-pull
74x09	Quad 2-input AND gate	4	Normal	Open-collector
74x10	Triple 3-input NAND gate	3	Normal	Push-pull
74x11	Triple 3-input AND gate	3	Normal	Push-pull
74x12	Triple 3-input NAND gate	3	Normal	Open-collector
74x13	Dual 4-input NAND gate	2	Schmitt trigger	Push-pull
74x4051	High-speed 8-channel analog multiplexer/demultiplexer	1	Analog	Analog
74x4052	Dual 4-channel analog multiplexer/demultiplexer	2	Analog	Analog
74x4053	Triple 2-channel analog multiplexer/demultiplexer	3	Analog	Analog

The x is a placeholder for the logic subfamily. For example, in 74LSxx the LS represent the low-power Schottky subfamily.

A company specific prefix may be added to the above part numbers depending on the manufacturer.

Prefix	Company
<none>	Nexperia, Phillips
CD	Texas Instruments
DM	National Semiconductor
ID	IDT
M	STMicroelectronics
MC	OnSemi
MM	National Semiconductor
NLV	OnSemi
SN	Texas Instruments
TC	Toshiba

Karnaugh Maps

Karnaugh maps are a way of simplifying combinational logic, often used before realising a combination equation into a number of gates to reduce the complexity.

Logic Simulators

CEDAR Logic Simulator is my personal favourite. Free, easy to use, colours the wires depending on their state, and allows for named nets as well as direct connections.

Example Logic Circuits

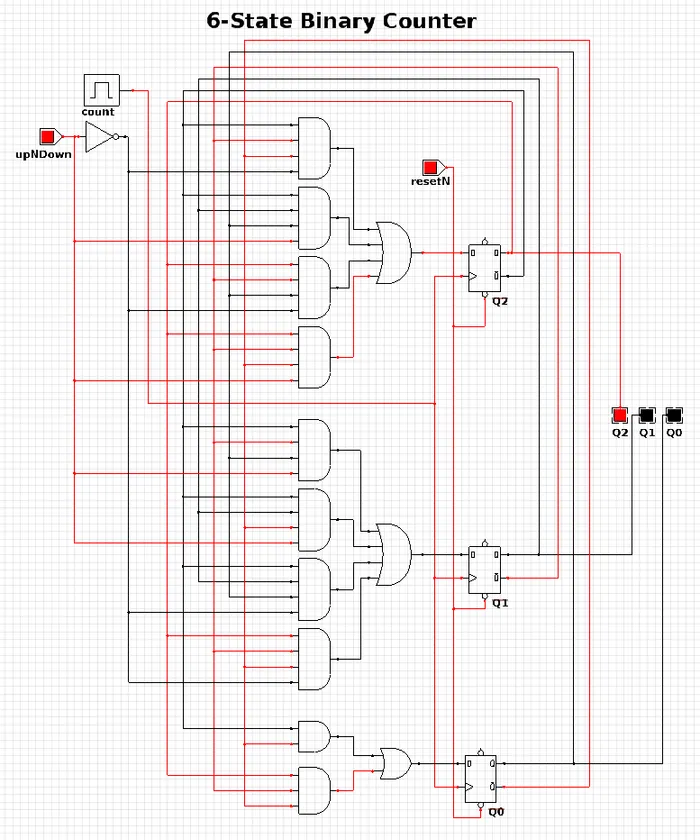
6-State Binary Counter

Category: Counter
Expression Style: Sum of Products
No. of Gates: 14
No. of Flip-flops: 3
1-Bit Inputs: 2 + reset
1-Bit Outputs: 3

Tested On:

• Simulation: Yes (CEDAR Logic Simulator)
• Hardware: Yes

Downloads: CEDAR Logic Simulator File

The 6-state binary counter is a counter which counts from 000 to 101 in the normal binary fashion before resetting back to 0. The output increments on every rising-edge of the count pulse, and the direction pin (upNDown) determines the count direction (when upNDown = 1, the counter goes from 000 to 101, when upNDown is 0 the counter goes from 101 to 000).

The flip-flop equations expressed as sums of products are:

$$\begin{align} Q_2 = \bar{Q_2}.\bar{Q_1}.\bar{Q_0}.\bar{y} + \bar{Q_2}.Q_1.Q_0.y + Q_2.\bar{Q_1}.Q_0.\bar{y} + Q_2.\bar{Q_1}.\bar{Q_0}.y \\ \\ Q_1 = \bar{Q_2}.\bar{Q_1}.Q_0.y + \bar{Q_2}.Q_1.\bar{Q_0}.y + \bar{Q_2}.Q_1.Q_0.\bar{y} + Q_2.\bar{Q_1}.\bar{Q_0}.\bar{y} \\ \\ Q_0 = \bar{Q_2}.\bar{Q_0} + Q_2.\bar{Q_1}.\bar{Q_0} \\ \\ \end{align}$$

Schematic of a six state binary counter.

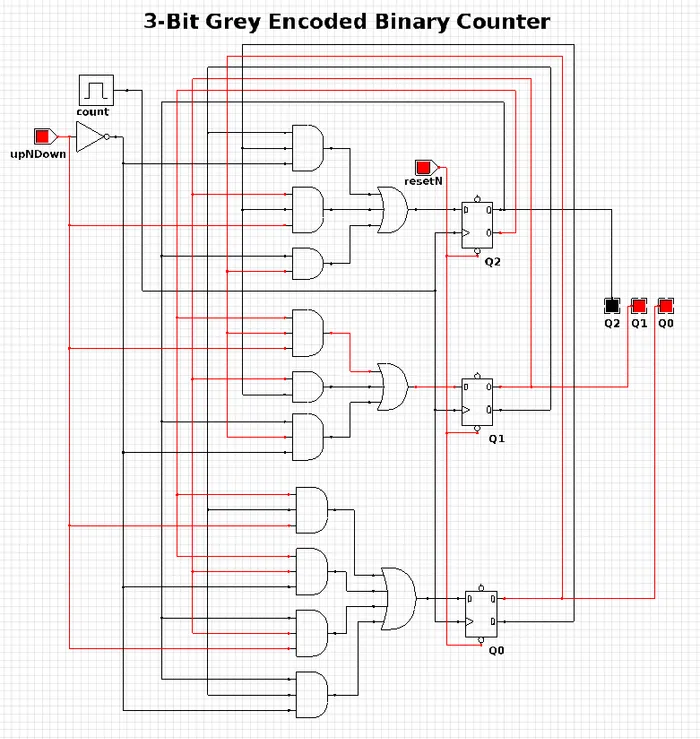
3-Bit Grey Encoded Counter

Category: Counter
Expression Style: Sum of Products
No. of Gates: 14
No. of Flip-flops: 3
1-Bit Inputs: 2 + reset
1-Bit Outputs: 3

Tested On:

• Simulation: Yes (CEDAR Logic Simulator)
• Hardware: Yes

Download: CEDAR Logic Simulator File

The 3-Bit Grey Encoded Counter is a counter that counts from 0 to 7 in binary in a grey encoded fashion. The counter increments on every rising edge of the bit ‘count’ and the direction bit ‘upNDown’ determines the direction of counting.

Schematic of a three-bit Grey encoded binary counter.

Footnotes

1. Wikipedia (2005, Aug 20). List of logic symbols. Retrieved 2021-10-25, from https://en.wikipedia.org/wiki/List_of_logic_symbols. ↩ ↩²

2. McAllister, Willy (2021). Digital logic gates. Spinning Numbers. Retrieved 2021-10-24, from https://spinningnumbers.org/a/logic-gates.html. ↩ ↩²

3. Maxim Integrated (2020). Glossary Definition For XOR Gate. Retrieved 2021-10-22, from https://www.maximintegrated.com/en/glossary/definitions.mvp/term/XOR%20Gate/gpk/1202. ↩

4. Wikipedia (2024, Aug 2). Apollo Guidance Computer. Retrieved 2024-08-21, from https://en.wikipedia.org/wiki/Apollo_Guidance_Computer. ↩

5. Wikipedia (2023, Apr 22). Transistor–transistor logic. Retrieved 2023-05-10, from https://en.wikipedia.org/wiki/Transistor%E2%80%93transistor_logic. ↩

6. Wikipedia (2023, Mar 12). NMOS Logic. Retrieved 2023-04-29, from https://en.wikipedia.org/wiki/NMOS_logic. ↩

7. Wikipedia (2023, Feb 17). CMOS. Retrieved 2023-04-29, from https://en.wikipedia.org/wiki/CMOS. ↩

8. Wikipedia (2023, Mar 20). XOR gate. Retrieved 2023-05-05, from https://en.wikipedia.org/wiki/XOR_gate. ↩

9. University of Utah: John and Marcia Price College of Engineering. ECE/CS 5710/6710 – Digital VLSI Design: Lab Assignment #3. Retrieved 2023-04-24, from https://my.eng.utah.edu/~kstevens/5710/lab3.pdf. ↩

10. Wikipedia (2022, Nov 22). Pass transistor logic. Retrieved 2023-05-05, from https://en.wikipedia.org/wiki/Pass_transistor_logic. ↩

11. Robert Keim (2018, Dec 26). Digital Design with Pass-Transistor Logic. All About Circuits. Retrieved 2023-05-09, from https://www.allaboutcircuits.com/technical-articles/digital-design-with-pass-transistor-logic/. ↩

12. University of Waterloo - ECE. ECE 637 - Lecture 11 - Pass-Transistor Logic. Retrieved 2023-05-09, from https://ece.uwaterloo.ca/~mhanis/ece637/lecture11.pdf. ↩ ↩²

13. Texas Instruments (1997, Nov). CDx4HC405x, CDx4HCT405x High-Speed CMOS Logic Analog Multiplexers and Demultiplexers (Datasheet). Retrieved 2021-10-20, from https://www.ti.com/lit/ds/symlink/cd74hc4051.pdf. ↩