Inductors

Inductors are passive, 2 pin electronic components which store energy as a magnetic field. They are made by coiling wire around a material (be it air, or something else). They are well used but due to their bulk, cost and usefulness, are not as common as resistors or capacitors in electronic circuits.

A 3.35uH 20A large inductor.

The mechanical equivalent of an inductor is mass. The larger the inductance, the larger the mass. This is when using the force-voltage equivalence.

Two inductances which are in close proximity they can couple with each, this is called mutual inductance. This is the basic principle behind a transformer.

Inductors are used in many things, including:

• Common-mode chokes
• Ferrite beads
• Transformers
• Switch mode power suppliers (e.g. buck and boost converters)
• Pi/T filters

How They Work

When current is flowing through an inductor, some electrical energy is converted and stored as magnetic energy in the inductors magnetic field. Inductors like staying at a constant current, and they “actively resist” current changes. They do this by generating a voltage across their terminals which resists the change in current.

The defining equation relating the voltage, inductance and change in current is:

$$v = L \frac{di}{dt}$$

where:
$v$ is the voltage across the inductor
$L$ is the inductance of the inductor
$\frac{di}{dt}$ is the instantaneous change in current through the inductor

Example

If you connected 12V across an inductor, initially there would be no current, as current cannot change instantaneously through an inductor. Then, because the voltage across the inductor is a constant 12V, the current through the inductor would rise linearly. The bigger the inductance, the slower the current would increase, as per the equation above. In a perfect world this would continue forever, but in reality either your power supply will current limit, your inductors magnetic core would saturate, or your inductor will start to overheat.

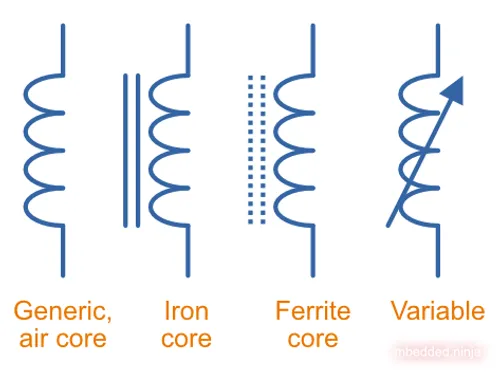
Schematic Symbols and Designator

There are a few common schematic symbols for an inductor. L is almost always used as the designator prefix on schematics, e.g. inductors will be named L1, L2, e.t.c. This is a placeholder for the reference: fig-schematic-symbols-of-inductors shows the symbols used for common sub-families of inductors. Not all circuit designers will be specific and use a special symbol to indicate iron/ferrite cored inductors (vs. air-cored inductors), and the generic symbol may be used for all types.

Schematic symbols for a range of the basic inductor sub-families.

Important Parameters

Inductance

• Symbol: $L$
• Units: Henries (or Henrys)¹ ($H$)

The main thing you care about! The inductance determines the relationship between the rate of change in current through the inductor and the inductors voltage. It determines the voltage the inductor will generate in response to a specific rate of current change. This parameter is used to calculate it’s impedance, for a given frequency.

K-factor

The K-factor (a.k.a.) coupling coefficient is a fractional value of the amount of flux linkage between two coils. It is not applicable for a single inductor, but is a useful property when describing transformers.

DC resistance

• Symbol: $DCR$
• Units: Ohms ($\Omega$)

The DC resistance is the resistance of the inductor’s coil of wire, measured at DC. You can use this to calculate resistive losses through the inductor. An ideal inductor has no DCR. The DC resistance of an inductor can be easily measured by a good quality multimeter or benchtop Ohm meter. For a fixed volume, a larger valued inductor usually has a higher DCR as it has a larger number of thinner guage turns.

Typical DC resistances range from $10m\Omega$ to $10\Omega$.

Saturation Current

• Symbol: $I_{sat}$
• Units: Amps ($A$)

The saturation current is the maximum current the inductor can take before it stops working like an inductor (it’s not a sudden point, but rather defined as when the inductance drops to a fixed percentage of it’s nominal value). Above this point, the magnetic field does not increase proportionally with the current (the core is “saturated”), and the apparent inductance of the inductor is decreasing. This also means that above the saturation current the current will rise/fall much faster, which can cause it to shoot up to dangerous levels. It is not the same thing as the rated current.

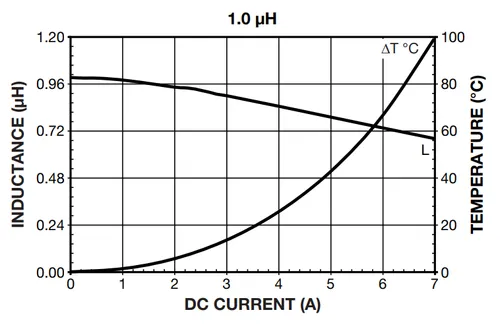
For example, Vishay Dale specified the saturation current for it’s IHLP-1212BZ-11 family (datasheet) of inductors as the current at which the inductance drops 20% down from the value at 0A (it’s rated inductance)². This is a placeholder for the reference: fig-inductance-vs-dc-current-vishay-ihlp1212bzer1r0m11 shows the inductance vs. DC current plot for the IHLP1212BZER1R0M11 inductor in this family. This inductor has a saturation current of 4.5A.

Plot of inductance vs. DC current for the Vishay Dale IHLP1212BZER1R0M11 inductor².

Typical saturation currents range from 10-100mA’s for small inductors, up to 1-10A for larger PCB mount inductors.

Rated current

• Symbol: $I_{rated}$
• Units: Amps ($A$)

The rated current is typically given as the amount of average current required to created a fixed temperature rise above ambient due to resistive losses in the copper winding. The temperature rise is usually 40°C. Inductors can usually handle current peaks above the rated current as long as the average is still less.

Self-resonant Frequency

• Symbol: $SRF$
• Units: Megahertz ($MHz$)

The self-resonant frequency of an inductor is the frequency at which the parasitic capacitance of the inductor resonates with the inductance, resulting in a very high impedance (e.g. open circuit)³. The inductor stops behaving like a inductor above the self-resonant frequency.

The below plot shows a plot of inductance vs. frequency for the Vishay Dale IHLP1212BZER1R0M11 inductor. The self-resonant frequency occurs where the inductance $L$ spikes at about 75MHz:

Plot of inductance vs. frequency for the Vishay Dale IHLP1212BZER1R0M11 inductor², highlighting the self-resonant frequency (SRF).

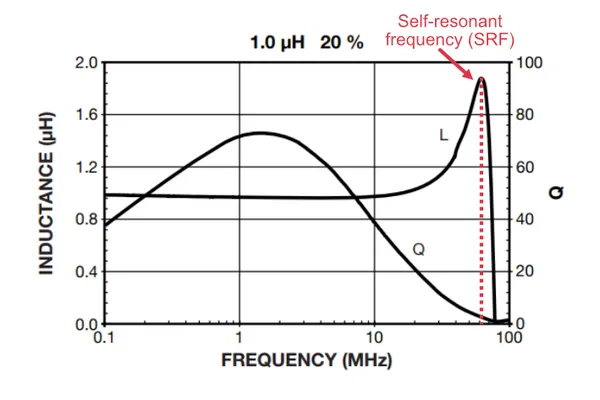
The equation for the SRF is⁴:

$$\begin{align} SRF = \frac{1}{2\pi \sqrt{LC}} \end{align}$$

where:
$L$ is the inductance in Henries
$C$ is the parasitic capacitance, in Farads
$SRF$ is the self-resonant frequency, in Hertz

The main contributor to the parasitic capacitance is the distributed capacitance between each coil windings.

Types Of Inductors

Ferrite Drum Core Inductors

Ferrite drum core inductors can be optionally shielded. They allow for high saturation currents and high inductances (due to having a large number of turns).

Toroidal Inductors

Flat Coil Inductors

Flat coil inductors have a very low profile (height from the surface of the PCB) allowing use in space-constrained designs. Flat coil inductors usually have a low number of turns, resulting in less inductance than ferrite drum core or toroidal inductors. The core is typically made up of powdered iron.

Metal Composite Inductors

Metal composite inductors (also called moulded power inductors) are made with metal powders moulded around copper windings at high pressure.

Internal construction of a metal composite inductor. Image by Kemet, retrieved from https://media.digikey.com/pdf/Data%20Sheets/Kemet%20PDFs/MPXV_Series_DS.pdf on 2020-11-30.

Air-cored Inductors

Air-cored inductors represent any inductor which contains no ferromagnetic material. This means that “air-cored” inductors also covers a range of inductors which use an insulator instead of air for the core, which includes materials such as glass or PTFE.

Advantages

• Unlike a ferro-magnetic cored inductor, an air-cored inductors inductance does not vary with the amount current that is flowing with it. Ferromagnetic cores work fine up until a point at which they saturate.
• Air-cores do not have any iron losses. This advantage becomes more significant with increasing frequency.

Disadvantages

• Air-cored inductors have to have more and/or larger turns to achieve the same inductance value as a ferro-magnetic core. This is because ferro-magnetic cores have a higher permeability than air.
• Air-cored inductors radiate more electromagnetic fields over a wider area, and also pick up more radiation. This is because ferro-magnetic-cores constrain the magnetic field lines better.

Ferrite Beads

See the Ferrite Beads page.

Common Core Materials

Air Core

Air core is used to describe any inductor which does not use a magnetic material for it’s core (so they may in fact, have something other than air for their core). Used in low inductance, RF applications because they lack any magnetic core to boost their inductance, but at the same time benefit from smaller core losses which can be significant in the RF spectrum. Go to the Air-Cored Inductors section for more info.

Powdered Ferrite Core

The powder is compressed into blocks before using (but don’t confuse these with solid ferrite core inductors). Very lossy (resistive) at high frequencies. Used to make ferrite beads.

Solid Iron (or Steel) Core

Used in low resistance, high inductance applications. Has a higher saturation current than air-cored inductors, but lower one than powdered iron cores.

Powdered Iron Core

Powered iron core inductors have a distributed air gap, which gives them a higher saturation current then solid iron cored inductors.

Metal Composite

While ferrite cored inductors seem to have similar current ratings (based of thermal performance) as their saturation current, metal composite inductors typically have a saturation current between 1-2x their current rating (e.g. a current rating of 3A, and a saturation current between 3-6A).

Inductors In Series And In Parallel

The behaviour of inductors when connected together in series and in parallel is exactly the same behaviour resistors exhibit, and exactly the opposite behaviour of what capacitors exhibit.

Inductors In Parallel

When two inductors are connected in parallel, the equivalent total inductance follows the inverse law, as long as there is no mutual coupling of their magnetic fields:

$$\begin{align} L_{total} = \dfrac{1}{\dfrac{1}{L1} + \dfrac{1}{L2}} \end{align}$$

It is usually easier to remember this equation as:

$$\begin{align} \dfrac{1}{L_{total}} = \dfrac{1}{L1} + \dfrac{1}{L2} \end{align}$$

This is a placeholder for the reference: fig-inductors-in-parallel-with-equation shows this:

Two inductors in parallel is the equivalent of one inductor whose inductance is given by the reciprocal equation in this image.

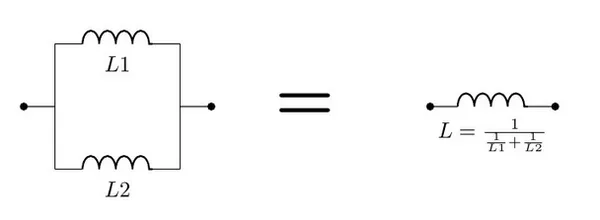
Inductors In Series

The equivalent inductance of two inductors connected in series is the sum of the individual inductances, as long as there is no mutual coupling of their magnetic fields.

$$\begin{align} L_{total} = L1 + L2 \end{align}$$

This is a placeholder for the reference: fig-inductors-in-series-with-equation shows this:

Two inductors in series are the equivalent of one inductor whose inductance is the sum of the individual inductances.

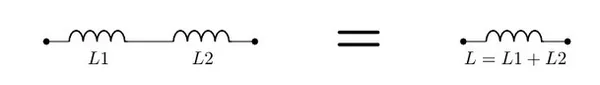
The Energy Stored In An Inductor

The energy stored in a inductor is given by:

$$\begin{align} E = \frac{1}{2}LI^2 \end{align}$$

where:
$E$ is the energy stored in the inductor, in Joules $J$
$L$ is the inductance of the inductor, in Henries $H$
$I$ is the current flowing through the inductor, in Amps $A$

This equation is only valid when the inductor is operating in it’s linear region, that is, before the current reaches the point where the magnetic field begins to saturate. Notice that it is similar to the equation for energy in a capacitor.

The Impedance Of An Inductor

Simple Model

An ideal inductor (no parasitic elements) has an impedance $Z_L$ given by:

$$\begin{align} Z_L = 2\pi fL \end{align}$$

where:
$Z_L$ = inductor’s impedance, in Ohms ($\Omega$)
$f$ = frequency of analysis, in Hertz ($Hz$)
$L$ = inductance of inductor, in Henries ($H$)

Note

Sometimes $X_L$ is used instead of $Z_L$. $X$ represents reactance (purely imaginary), whilst $Z$ is for impedance (which may contain real and imaginary parts). For a simple inductor with no parasitic elements the reactance and impedance is the same, i.e. $X_L = Z_L$.

This shows that the impedance goes up as the frequency goes up. At DC levels, the inductor has no impedance and acts like a short-circuit, while at high frequencies the inductor approaches an open-circuit.

You may also see this written as:

$$\begin{align} Z_L = \omega L \end{align}$$

where:
$\omega$ = radian frequency (rad/s) (which is equal to $2\pi f$)

Note

Impedance, although measured in Ohms, is not the same as resistance. A resistance converts the energy into heat, the impedance of the inductor however cause the energy to be stored in it’s magnetic field, which is returned to the circuit when the current falls.

For a more accurate but complex model, see the Parasitic Model section.

Parasitic Model

An inductor with parasitic components may be modelled by:

$$\begin{align} Z_L = \frac{1}{ \frac{1}{R_P} + \frac{1}{j \omega L + R_S} + j \omega C_P } \end{align}$$

where:
$Z_L$ = inductor’s impedance ($\Omega$)
$R_P$ = parasitic parallel resistance (which is negligible for most simulations) ($\Omega$)
$\omega$ = frequency of analysis ($rad/s$)
$L$ = inductance of inductor ($H$)
$R_S$ = parasitic series resistance ($\Omega$)
$C_P$ = parasitic parallel capacitance ($F$)

The main parasitic components are the series resistance ($R_S$) and the parallel capacitance ($C_P$). The series resistance arises from the resistance of the coil of wire which makes up the inductor. This thinner and longer the coil, the larger this resistance. The parallel capacitance is due to coil windings being very close to one another, each coil forming small capacitors to surrounding coils. This small capacitors can be lumped together and form the parallel capacitance.

This model is a pretty good representation for most simulation purposes, and gives that characteristic decrease in performance (non-inductor-like behaviour) at high-frequencies.

Typical values might be:

• $R_P = 0\,\Omega$
• $L = 1\,uH$
• $R_S = 10\,m\Omega$
• $C_P = 10\,pF$.

Inductor Networks

Inductors In Parallel

Inductors in parallel behave just like resistors in parallel.

$$\begin{align} \frac{1}{L_{eq}} = \frac{1}{L_1} + \frac{1}{L_2} + \ldots + \frac{1}{L_N} \end{align}$$

Inductors In Series

Inductors in series behave just like resistors in series.

$$\begin{align} L_{eq} = L_1 + L_2 + \ldots + L_n \end{align}$$

Inductor Kickback

Inductor kickback is when an inductor the current through an inductor is quickly stopped, usually by making an open circuit. Because inductors “want to keep the current flowing”, they generate a very large voltage spike in attempt to keep the current going. This large voltage spike can jump switch gaps, fry MOSFETs, destroy other sensitive circuitry, and give people dangerous shocks.

A more technical way of looking a kickback is by analysing the voltage-inductance equation. From this is should be obvious that the inductors voltage is proportional to the change in current. Making an inductor open-circuit is creating a very large change in current, and hence it produces a very large voltage spike.

Inductor kickback is a significant design issue when using relays or motors.

Saturation Current

Inductors only behave like inductors over a limited current range. As the current continues to increase, the apparent inductance of the inductor decreased. Above a certain current, they become what is called saturated.

Saturation is the state reached when an increase in applied external magnetizing field H cannot increase the magnetization of the material any further.

This is a placeholder for the reference: fig-inductance-vs-current-graph-wurth-7447789003-3.3uh shows a typical inductance vs. current curve for a ferrite core, SMD inductor that could be used on a 3A SMPS design. It’s rated saturation current is 4.2A. Notice how after the current increases beyond this point, the inductance of the inductor drops of rapidly.

Inductance vs. current graph of the Wurth 7447789003, a 3.3uH ferrite SMD inductor with a specified saturation current of 4.2A.

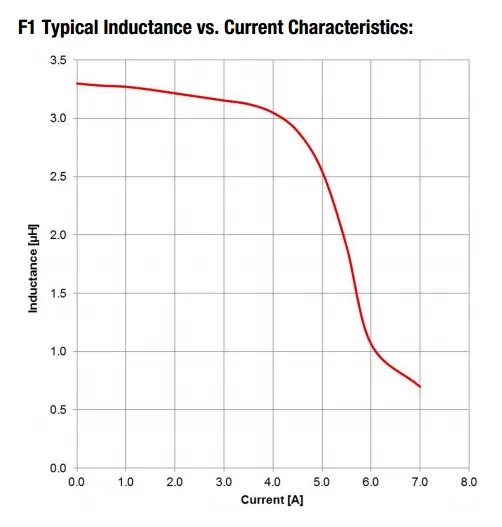
As governed by the basic induction equation, applying a constant voltage across an inductor will lead to a linear increase in current. This will be the case until the saturation point, at which the current will begin to increase more rapidly, until is reaches a limit determined only by the DC resistance of the windings.

Reaching saturation is not always a bad thing. Saturation is desirable in self-switching power supplies, timing circuits and blocked oscillators, and saturable-core transformers (e.g. arc welding). It is not desirable in typical SMPS, or power/signal transformers.

Rated Current

The rated current of an inductor is the maximum DC current allowed before the inductor gets”too hot”. “Too hot” is usually defined as a certain temperature rise above ambient (e.g. $40^{\circ}C$) when the inductor is mounted using a standard footprint on a standard PCB; again, both defined by the manufacturer.

Saturation Current vs. Rated Current

There are usually two maximum current ratings on an inductor’s datasheet, the saturation current and the rated current.

Confusing? The most simple Simon design approach is to pick the lower maximum current of the two and treat that as the maximum current allowed through the inductor. A seasoned inductor sensei will realise that the rated current is not applicable to short current peaks, and so it is safe to exceed this for brief periods of time, as long as the saturation current is not exceeded (disclaimer: in some cases, even exceeding the saturation current limit is o.k. or even desirable, but see the Saturation Current section for more info on this.

How To Measure Inductance In An Electronics Lab

Inductor markings can be confusing (or completely absent!), making it hard to determine the part number and inductance of a particular inductor. Additionally, basic multimeters have no ability to measure inductance. Luckily, there are many ways to measure inductance in a laboratory setting.

Measuring Inductance with a Signal Generator and Oscilloscope

One way to measure the inductance of an inductor is with a signal generator and oscilloscope⁵.

1. Set the signal generator to:

   • Waveform: Sine wave
   • Voltage: 1 V peak-to-peak
   • Frequency: 10 kHz
   • Output type: High-Z

2. Connect the oscilloscope to the signal generator and measure the open-circuit voltage. It should be about 1 V peak-to-peak. Record down the exact peak-to-peak value, as signal generators are not usually that accurate with their voltages!

   

   Tip

   If you read 2V peak-to-peak, you probably have the signal generators output type set to 50Ω, which means it doubles the voltage. Switch to high-Z or change the voltage to 500mV peak-to-peak to compensate.

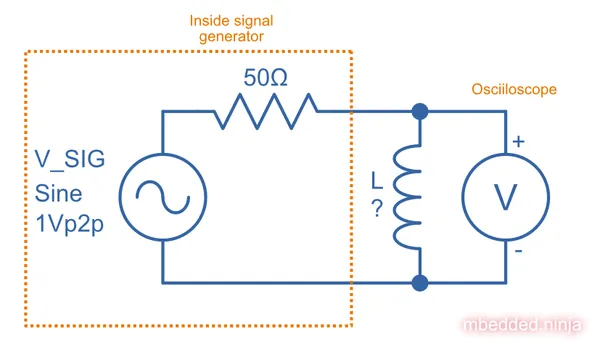
3. Now connect the inductor to the signal generator, whilst still measuring the voltage with the oscilloscope (this will be the output voltage of the signal generator, as well as the voltage across the inductor). The circuit should look like This is a placeholder for the reference: fig-inductor-measurement-with-sig-gen-and-oscilloscope-02:

   

4. Adjust the frequency of the signal generator until the peak-to-peak voltage across the inductor is half the measured open-circuit peak-to-peak voltage.

5. Calculate the inductance! It is equal to:

   $$\begin{align} L = \sqrt{\frac{1}{3}} \cdot \frac{50\,\Omega}{2\pi f} \end{align}$$

   where:
   $f$ is the frequency in Hertz at which the inductors peak-to-peak voltage was half the signal generators open-circuit peak-to-peak voltage
   $50\,\Omega$ is the output impedance of the signal generator (measure and tweak this value for a more accurate calculation)
   $L$ is the calculated inductance, in Henries
   

   Caution

   The above method only works well for inductors which have a low series resistance⁵.

How It Works

The internal resistance of the signal generator $50\,\Omega$ and the inductance form a voltage divider. The impedance of the resistor stays constant at $50\,\Omega$ no matter the frequency, but the impedance of the inductor does change with frequency ($Z_L = X_L = \omega L$). You vary the frequency until the voltage at the mid-point of the voltage divider is half the total voltage, which means that the impedances of the resistor and inductor are the same.

We arrive at the equation for the inductance by using the voltage-divider rule for a complex circuit:

$$\begin{align} \left| \frac{V_{SCOPE}}{V_{SIG}} \right| = \left| \frac{j\omega L}{R + j\omega L} \right| \end{align}$$

Simplifying:

$$\begin{align} \left| \frac{V_{SCOPE}}{V_{SIG}} \right| &= \left| \frac{j\omega L}{R + j\omega L} \cdot \frac{R - j\omega L}{R - j\omega L} \right| \nonumber \\ &= \left| \frac{j\omega RL + \omega^2 L^2}{R^2 + \omega^2 L^2} \right| \end{align}$$

Now let’s separate the equation into a real and imaginary part:

$$\begin{align} \left| \frac{V_{SCOPE}}{V_{SIG}} \right| &= \left| \frac{\omega^2 L^2}{R^2 + \omega^2 L^2} + j\frac{\omega RL}{R^2 + \omega^2 L^2} \right| \\ \end{align}$$

Now we can take the magnitude of this and simplify:

$$\begin{align} \left| \frac{V_{SCOPE}}{V_{SIG}} \right| &= \sqrt{ \frac{\omega^4 L^4}{(R^2 + \omega^2 L^2)^2} + \frac{\omega^2 R^2L^2}{(R^2 + \omega^2 L^2)^2} } \nonumber \\ &= \frac{\sqrt{\omega^4 L^4 + \omega^2R^2L^2}}{R^2 + \omega^2L^2} \nonumber \\ &= \frac{\sqrt{\omega^2 L^2(R^2 + \omega^2L^2)}}{R^2 + \omega^2L^2} \nonumber \\ &= \frac{\omega L}{\sqrt{R^2 + \omega^2L^2}} \\ \end{align}$$

We’ve got it to a point where it is as about as simple as you can write it! Next up, let’s substitute $\left| \frac{V_{SCOPE}}{V_{SIG}} \right|$ with $\frac{1}{2}$), as this was the condition we were tweaking the frequency for (peak-to-peak voltage measured across inductor by the oscilloscope was half the peak-to-peak voltage generated by the signal generator).

$$\begin{align} \frac{1}{2} &= \frac{\omega L}{\sqrt{R^2 + \omega^2L^2}} \nonumber \\ \frac{1}{4} &= \frac{\omega^2 L^2}{R^2 + \omega^2L^2} \nonumber \\ R^2 + \omega^2 L^2 &= 4\omega^2 L^2 \nonumber \\ R^2 &= 3 \omega^2 L^2 \nonumber \\ L^2 &= \frac{1}{3} \frac{R^2}{\omega^2} \nonumber \\ L &= \sqrt{\frac{1}{3}} \frac{R}{\omega} \end{align}$$

Now we just sub in $2\pi f = \omega$ to get the final equation:

$$\begin{align} L &= \sqrt{\frac{1}{3}} \frac{R}{2\pi f} \end{align}$$

Manufacturer Part Numbers

• DR1050: Series of inductors by Eaton (previously Cooper Bussmann).
• NRx: Popular series of inductors from Taiyo Yuden. x denotes the coating resin, options are NR, NRH, NRS and NRV. The series contains a number of different SMD package sizes and inductances.

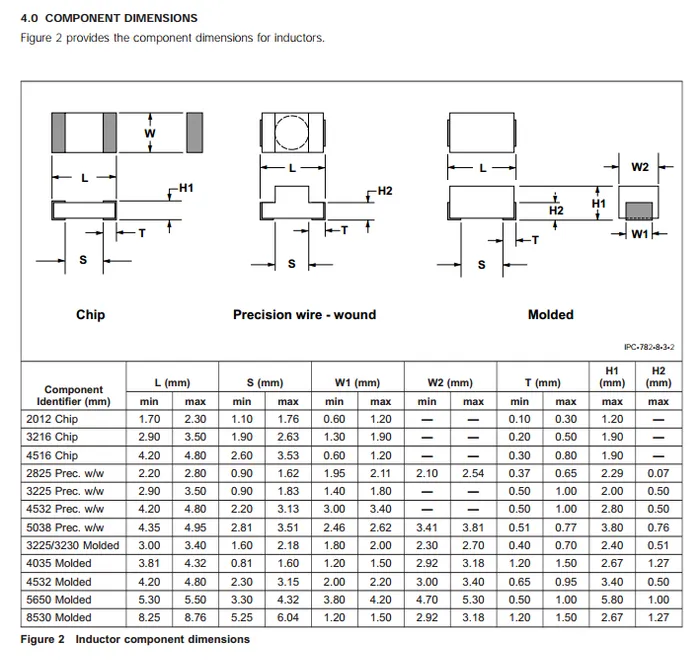
Inductor Packages

Unfortunately for the PCB designer, almost all SMD inductor packages are non-standard and unique to the manufacturer and series.

Standard dimensions for three different types of SMD inductor packages. Image from the IPC-SM-782 standard.

Footnotes

1. Wiktionary. henry. Retrieved 2022-07-10, from https://en.wiktionary.org/wiki/henry. ↩

2. Vishay Dale. _IHLP-1212BZ-11: IHLP Commercial Inductors, Low DCR Series (datasheet). Retrieved 2022-07-11, from https://www.vishay.com/docs/34289/lp12bz11.pdf. ↩ ↩² ↩³

3. everythingRF. What is Self Resonant Frequency (SRF) in Inductors?. Retrieved 2022-07-11, from https://www.everythingrf.com/community/what-is-self-resonant-frequency. ↩

4. Coilcraft (2003, Sep 16). Document 363-1: Measuring Self Resonant Frequency. Retrieved 2022-07-11, from https://www.coilcraft.com/getmedia/8ef1bd18-d092-40e8-a3c8-929bec6adfc9/doc363_measuringsrf.pdf. ↩

5. Ronald Dekker. A Simple Method to Measure Unknown Inductors. DOS4Ever. Retrieved 2022-07-06, from https://www.dos4ever.com/inductor/inductor.html. ↩ ↩²